• EigenValue Decomposition
  • Case Study
  • 与Single Value Decomposition的关系
• Singular Value Decomposition
  • 预备知识
  • 最佳低秩逼近矩阵
  • 计算SVD
  • 应用
• ==Case Studies D==
  • PCA
• Iterative Methods For Linear Equations
  • GD for Linear Equations Ax=b
  • CG for Linear Equations Ax=b
• Unconstrained Optimization
  • 预备知识
    • 梯度与求导
    • 凸函数
  • Gradient Descent
  • Newton’s Method
  • BB Method
  • BFGS
  • ==总结==
• Case Studies E
  • K-means
    • QR Algorithm on a Tridiagonal Matrix
    • QR Decomposition
    • LU Decomposition
    • Basic Operations of Matrix
    • 其他

This is my course note taken in Chinese.

EigenValue Decomposition

Case Study

• Page - Rank
• Spectral Clustering（重要）
  • 给你一个图，你要知道怎么分割
  • 要知道Laplacian
  • Normalized也要知道

与Single Value Decomposition的关系

• $A=U\Sigma V^T$
• 利用$A^TA=V\Sigma U^TU\Sigma V^T=V\Sigma^2V^T$

Singular Value Decomposition

预备知识

• SVD的形式：$A=U\Sigma V^T$

  • $U\in R^{\rm mxn}, \Sigma\in R^{\rm nxn}, V\in R^{\rm nxn}$
  • U和V是正交阵，$\Sigma$是对角阵，且$\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_n \ge 0$
    • matlab的svd出来的$\Sigma$矩阵就已经是排好序的了。
    • 特征值分解不一定存在，但是奇艺值分解一定存在。
    • 当A为对称正定矩阵的时候，特征值与奇艺值一样。

• 形式 $A=\left(\begin{array}{c}u_1,\cdots,u_n\end{array}\right)\left(\begin{array}{ccc}\sigma_1 &&\\ &\dots& \\ &&\sigma_n\end{array}\right)\left(\begin{array}{c}v_1^T\\ \vdots \\ v_n^T\end{array}\right)=\sum_{i=1}^n \sigma_i u_iv_i^T$

  • $AV=U\Sigma$ and $Av_i =\sigma_i u_i$
  • $rank(A)=r$等价于$\sigma_r >0, \sigma_{r+1}=0,\cdots, \sigma_n=0$（可降维成r阶

• ==show==性质

  • $|A|_2 = \sigma_1$
  • $|A|_F=\sqrt{\sigma_1^2+\cdots+\sigma_n^2}$
  • $k(A)=\frac{\sigma_1}{\sigma_n}$ 如果$\sigma_n >0$
  • $k(A^TA)=(k(A))^2$
  • $A^{-1}=\sum_{i=1}^n \sigma_i^{-1} u_iv_i^T$

最佳低秩逼近矩阵

• 只选择奇异值最大的r个

• $$A_r = \sum^r_{i=1}\sigma_iu_iv_i^T$$

  ​

• 关于矩阵的2范数和F范数的表示的问题还需要再掌握

计算SVD

• 若A是方阵
  • 
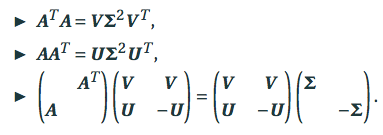
  • 此时SVD可以转换成$A^TA$或者$AA^T$的特征值分解来求
    • 因为$A^TA=V\Sigma^2 V^T$的形式和特征值分解的$A=T\Lambda T^T$的形式一样，利用特征值分解即可求出$\Sigma^2$和$V$，再通过A即可求U
• 若A不是方阵
  • 先把A转换成B，B是上三角的二对角矩阵，才能==保证==$B^TB$是三对角对称矩阵
  • 对$B^TB$ 进行QR分解

应用

• 解最小二乘法
  • 问题：find $x$ such that $f(x)=|Ax-b|_2^2$ is minimized
  • 转换：$A^TAx=A^Tb$
  • 应用SVD：$\Sigma V^T x=U^Tb$
• 图像压缩
• 矩阵完整化

==Case Studies D==

PCA

• 内积定义：$<A,B>=\sum_{i=1}^m \sum_{j=1}^n a_{ij} b_{ij}$
• 正交投影的概念
• 步骤：
  • 先计算$\bar x$和$\bar X$，$\bar X = (x_1-\bar x, \cdots, x_m - \bar x)$
  • 然后计算$\bar X$的SVD分解，$\bar X= U\Sigma V^T$
  • 令$Q=(u_1,\cdots,u_k)$，最大的k个奇艺值对应的k个奇艺值向量 （此处降秩到k
  • 对于一个新的$x$，计算正交分解$QQ^Tx$

Iterative Methods For Linear Equations

• 前提：A is symmetric positive definite matrix （则可以用Cholesky Decomposition
• 目的：解$Ax=b$
• 经过求导转换后，解$Ax=b$相当于解$\min \frac{1}{2}x^TAx-b^Tx=\min f(x)$

GD for Linear Equations Ax=b

• 步骤

  

• 记号：$r_k=-\nabla f(x_k)=b-Ax_k$

• ==证明==$\alpha_k=\frac{r_k^Tr_k}{r_k^T A r_k}=\arg \min h(\alpha),h(\alpha)=f(x_k+\alpha r_k)$

• 终止条件：$|r_k|_2$足够小

• ==证明==收敛速度

  • $f(x_{k+1})-f(x_)\le\rho f(x_{k+1})-f(x_)​$，其中$\rho=1-\frac{1}{k(A)}​$
  • 当条件数$k(A)$越大的时候，收敛速度越快

CG for Linear Equations Ax=b

• $p_k=-\nabla f(x)+\beta_k p_{k-1}$

• 步骤

  

• ==正交性和共轭正交性==

  • $<r_k,r_j>=0,\,\, <r_k,p_j>$ for all $j<k$
  • $<p_k,Ar_j>=0,\,\, <p_k,Ap_j>$ for all $j<k$

• $Ax=b$，需要A对称且正定

  • ==问题==：for general linear equation, how to solve it using CG method? ( A is general matrix, invertible)
  • $AX=b, A=M-N$，$X_{k+1}=M^{-1}NX_k+b$ ？？？

• 前n步之内一定可以收敛到真解（==why？==需要掌握），收敛比GD快。

  • $ {r_0,r_1,\cdots}$ are always orthogonal

• 更有效率的步骤

  

• preconditioning的CG不做要求，思路：condition number越小越好。

Unconstrained Optimization

预备知识

• 全局最优和局部最优的概念

梯度与求导

• 梯度的定义 $\nabla f(x)=\left(\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \vdots \\ \frac{\partial f}{\partial x_n}\end{array}\right)$

• Hessian的定义 $\nabla^2f(x)=\begin{bmatrix}\frac{\partial^2 f(x)}{\partial x_1^2} & \frac{\partial^2 f(x)}{\partial x_1\partial x_2} & \cdots & \frac{\partial^2 f(x)}{\partial x_1\partial x_n} \\ \frac{\partial^2 f(x)}{\partial x_2 \partial x_1} & \frac{\partial^2 f(x)}{\partial x_2^2} & \cdots& \frac{\partial^2 f(x)}{\partial x_2\partial x_n} \\ \vdots & \vdots& \cdots & \vdots \\ \frac{\partial^2 f(x)}{\partial x_n \partial x_1} & \frac{\partial^2 f(x)}{\partial x_n \partial x_2} & \cdots& \frac{\partial^2 f(x)}{\partial x_n^2} \end{bmatrix}$

• 矩阵的==求导规则== $\partial X^T=(\partial X)^T\\ \partial (X+Y)=\partial X+\partial Y\\ \partial (XY)=(\partial X)Y+X(\partial Y)\\$

  

  

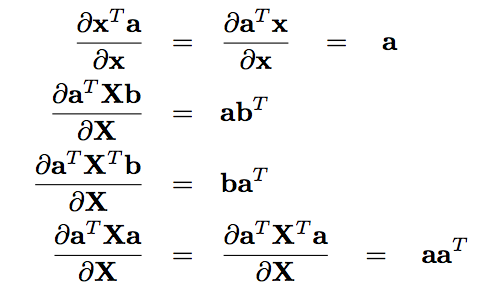
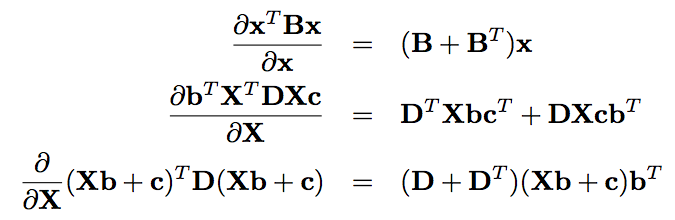
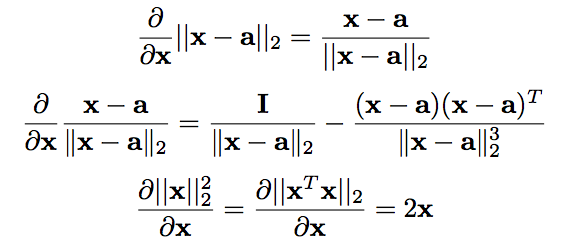
• 关于梯度和Hessian的必要和充分条件，注意一个是半正定，一个是正定。

  • 如果是局部最小，则：一阶导数为0，二阶导数是==半正定==。
  • 如果一阶导数为0，二阶导数是==正定==，则：局部最小。

凸函数

• 定义

  • $f(\lambda x+(1-\lambda)y)\le \lambda f(x)+(1-\lambda)f(y)$

  • 强凸函数

    • $f(x)-\frac{m}{2}|x|_2^2$ is convex for some $m>0$

    • ==总结==

      • f is convex if and only if f′′(x) ≥ 0 for all x.

        f is strongly convex if and only if f′′(x) ≥ m > 0 for all x.

      • 在问你一道题是不是convex还是strong convex的时候，做法就是先去求倒数，然后求倒数的最小值，看能不能找到m。

• 判断方法

  • 一阶导数满足$f(y)\ge f(x)+\nabla f(x)^T(y-x)$ $\Longleftrightarrow$ 凸函数
  • 二阶导数半正定 $\Longleftrightarrow$ 凸函数

• 性质

  • 全局最优就是局部最优
  • 证明==check this==

Gradient Descent

• 步骤

  

• 关于步长的选择

  • 可以是一个fixed的值

  • 也可以是backtracking line search的方法去迭代找到那个$\alpha$

    • $\alpha_k=\arg \min _{\alpha} f(x_k -\alpha \nabla f(bx_k))$

    • 算法

      

• 还用非常非常长的片段去证明了梯度下降的收敛性

  • ==Analysis==的部分全部没看

Newton’s Method

• 前提
  • f(x)为强凸函数
• 步骤
  • 
  • Backtracking每次都从$\alpha=1$ 开始
  • 由于p中已经包含了负号，所以在迭代x的时候用的+号
• ==例子==（期末考算法往往就是要你迭代几次
  • A special example $f(x)=\frac{1}{2}x^TAx-b^Tx$. What is the iteration of Newton’s method with stepsize $\alpha_k= 1$?
• 对比
  • GD只用到了一阶导数，而牛顿法用到了二阶导数
  • 与GD比起来，相当于每一次都要去解一个Hessian方程，所以计算成本很高（虽然收敛更快，所以这里有一个tradeoff
• 还对于牛顿法的收敛性进行了证明
  • ==Analysis==的部分全部没看

BB Method

• 目的：之前牛顿法每一次都要去解一个Hessian方程，计算成本较大，所以我们可以选取一个近似的Hessian矩阵来当成stepsize，降低计算成本。

• 缺点：用一个identity matrix来近似，虽然也有效，但是较为粗略。 $\alpha_k I \approx \nabla^2f(x_k)^{-1}$

BFGS

• 目的：找到一个更精确的近似Hessian矩阵的方式。

• 方法：满足两个条件，求导。

• 优点：$H_k$是由前一步的$H_{k-1}$更新得到的，计算比较方便。

• 步骤

  

• 记号

  • $s_{k-1}=x_k-x_{k-1},y_{k-1}=\nabla f(x_k)-\nabla f({x_{k-1}})$
  • 
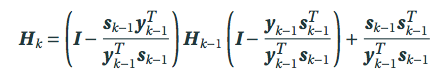
  • $H_0$可以选择I

• $H_k$的性质==证明很容易考到！==

  • 

    ​

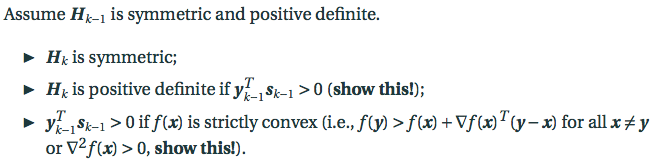
==总结==

• 关键在于抓住迭代的通式$x_{k+1}=x_k+\alpha p_k$
• 改变步长$\alpha$
  • backtracking line search
  • BB stepsize
• 改变下降方向$p_k$
  • GD：$p_k=-\nabla f(x_k)$
  • CG：$p_k=-\nabla f(x)+\beta_k p_{k-1}$
  • NM：$p_k=-\nabla^2 f(x_k)^{-1} \nabla f(x_k)$
  • BFGS：$p_k=-H \nabla f(x_k)$

Case Studies E

K-means

• 背景：n个数据点${X_i}{i=1}^n$，k个聚类中心${c_j}{j=1}^k$

• 目标：$E(c)=minJ(c,\gamma)=\sum_{j=1}^k\gamma_{ij}\parallel x_i-c_j\parallel_2^2$

  • 如果$x_i$属于类j，则$r_{ij}=1$，否则$r_{ij}=0$
  • $\sum_{j=1}^k \gamma_{ij}=1$，即每一个数据点属于且仅属于某一类

• 问题：找到如此定义的$E(c)$的全局最优是NP-hard的。

• 解决：Lloyd’s Algorithm

  • 将$x_i$分给离它最近的那个聚类中心$c_j$

    • 即：$r_{ij}=1$如果$c_j$是离$x_i$最近的，否则为1

  • 确定好了$r_{ij}$之后再重新计算聚类中心（该中心为属于该类的所有点的平均点

    • $c_j=\frac{1}{n_j}\sum_{r_{ij}=1}x_i$
    • ==这里注意证明== $c_j=\arg \min_\mu \sum_{r_{ij}=1}\parallel x_i-\mu\parallel_2^2$

  • 此时对于重新分类后的聚类中心有 $E(c)=\sum_{i=1}^n\sum_{j=1}^k \gamma_{ij}\parallel x_i-c_j\parallel^2=\sum_{j=1}^k \sum_{i=1}^n \gamma_{ij}\parallel x_i-c_j\parallel^2 \\=\sum_{j=1}^k \sum_{\gamma_{ij}=1}\parallel x_i-c_j\parallel^2$

• 收敛性证明

  • 因为$c_j’=\frac{1}{n_j}\sum_{r_{ij}=1}x_i$

  • 所以存在$ \sum_{\gamma_{ij}=1}\parallel x_i-c_j’\parallel^2 \le \sum_{\gamma_{ij}=1}\parallel x_i-c_j\parallel^2$

  • 对于$c’$决定的$r_{ij}’$则成立 $E(c')=\sum_{i=1}^n\sum_{j=1}^k \gamma_{ij}'\parallel x_i-c_j'\parallel^2 \le \sum_{i=1}^n\sum_{j=1}^k \gamma_{ij}\parallel x_i-c_j'\parallel^2 \\=\sum_{j=1}^k \sum_{\gamma_{ij}=1}\parallel x_i-c_j'\parallel^2 \le E(c)$

  • 可见，$E(c)​$的确是在随着迭代减小的。

• 问题：容易因为cluster center选择的不同而陷入不同的最优值，因为non-convex

QR Algorithm on a Tridiagonal Matrix

• 用Householder transformation将A转换成三对角矩阵
• $A=QR, \bar A=RQ$，若A为三对角，证明$\bar A$也应该为三对角

QR Decomposition

• Q orthogonal matrix proof: $I-2QQ^T$ also orthogonal
• 三种QR的算法需要掌握
• 可以出很多套定义的问题，但前提是你要明白定义啊
• 与Cholesky decomposition 联系起来出题
• Householder transformation 也有很多可以考的东西

LU Decomposition

• 作用：方便解线性方程
• Gaussian Elimination转换成U/L
• 如何compute LU
• 不是所有的矩阵都有LU，需要用pivoting
• 不涉及Case Study

Basic Operations of Matrix

其他

• 算法的考法就是让大家写几步推导
• 高老师讲的部分不考
• show、why之类的ppt上的地方要重要，然后讲过的题目也非常重要！
• 不能用计算器