• Chap 7 - Introduction to Statistical Inference
  • Population
  • Sample
  • Parametric Models
  • Statistic
  • Fundamental concepts in statistical inference
    • Point Estimation
    • Confidence Sets
    • Hypothesis testing
  • Nonparametric models and Empirical distribution functions
    • Nonparametric model
    • Empirical Distribution Functions
• Exercise 5
  • 构造estimator并求其相关性质
  • 经验分布
• Chap 9 - Point Estimation
  • Methods of Moments Estimation
  • Maximum Likelihood Estimation
    • Likelihood
    • Maximum Likelihood Estimation
    • Numerical computation of MLEs
      • Newton-Raphson Scheme/Newton Method
      • The Fisher Scoring method
      • Differences between NM and FSM
  • Evaluating Estimation
    • Fisher Information
      • Cramer-Rao Inequality
      • Asymptotic Properties of MLEs
• Exercise 6
  • 求MLE及其性质
  • Information
• Chap 10 - Hypothesis Testing (I)
  • General setting of hypothesis test
  • Two types of errors
  • The Wald test
  • $\chi^2$ Distribution
  • Confidence Interval for $\sigma^2$
  • t Distribution
  • An important property of normal samples
  • Accurate confidence interval for mean
  • 看《概率论》书籍的补充【表格总结】
  • ==Most Powerful Tests and Neyman-Pearson Lemma==
• Exercise 7
  • 纯构造置信区间
• Chap 11 - Hypothesis Testing (II)
  • Likelihood Ratio Tests
    • Asymptotic Distribution of Likelihood ratio test statistic
  • The permutation test
  • $\chi^2$ test
    • Goodness of fit test
    • Test for independence of two discrete random variables
    • ==Test for several binomial distributions==
    • Test for rxc tables - a general description
• Exercise 8

This is my course note taken in Chinese.

Chap 7 - Introduction to Statistical Inference

Population

• 未知

Sample

• 已知、随机、iid

Parametric Models

• 我们假定总体符合一个分布$F(\cdot ; \theta)$，这个分布是我们熟悉的分布（比如：norm），而我们不知道的是分布的参数$\theta$。
• 在参数模型中，我们倾向于去估计这个$\theta$，一旦这个参数被确定下来，我们就知道了该分布的所有信息。

Statistic

• 对于随机的样本定义的一个已知的函数
• 已知意味着，函数表达式中不能出现未知的$\theta,\mu$等，而只能出现已知的$X_i$

Fundamental concepts in statistical inference

Point Estimation

• $$\hat \theta = g(X_1,\cdots,X_n)$$

• 评价estimator的指标：

  • $\mid \hat \theta-\theta\mid$

  • Mean Square Error $MSE(\hat \theta)=E\{(\hat \theta-\theta)^2\}=\{Bias(\hat \theta)\}^2+Var(\hat \theta)\\ Bias(\hat \theta)=E(\hat \theta)-\theta$

  • The Standard Error $\widehat {SE(\hat \theta)}=\widehat {\{Var(\hat \theta)}\}^{1/2}$ an estimator for the standard deviation ${Var(\hat \theta)}^{1/2}$

  • Consistency $\hat \theta \rightarrow \theta$

• estimator的渐近正态性 $(\hat \theta - \theta)/SE(\hat \theta) \rightarrow N(0,1)$

Confidence Sets

• 目的：表示估计的不确定性

• Confidence Interval

  • 含义：盖住真值的概率（注意主动被动）

  • Confidence level: $1-\alpha$

  • 渐近正态的estimator成立置信区间 $(\hat \theta - \theta)/SE(\hat \theta) \rightarrow N(0,1)\\ (\hat \theta-Z_{\alpha/2}SE(\hat \theta),\hat \theta+Z_{\alpha/2}SE(\hat \theta))$

  • 在这一章中讲的置信区间都还比较简单，只是利用CLT去构造一个正态的。

Hypothesis testing

• 问题：是否能够有足够的证据拒绝零假设

Nonparametric models and Empirical distribution functions

Nonparametric model

• 并不假定F为何种分布，而是直接对于F进行估计和检验

Empirical Distribution Functions

• $I(X_i \le x)$是属于Bernoulli分布的一个随机变量，$p=F(x)$

Exercise 5

构造estimator并求其相关性质

• 先按照该统计量在分布中的定义和性质写出他的原表达式（e.g. Bernoulli的方差是p(1-p)，均值是p）
• 这里可能会用到均值和方差的那些计算公式（e.g. $Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$）
• 然后利用plug in

经验分布

• 天生就适合与Bernoulli相结合，因为$I(X_i \le x)$定义上就是个Bernoulli的分布
• ==分清楚Bernoulli和Binomial==

Chap 9 - Point Estimation

• 目的：估计参数模型中的参数

Methods of Moments Estimation

• k阶矩（Moment） $\mu_k=\mu(\theta)=E(X^k)$

• k阶样本矩 $M_k=\frac{1}{n}\sum_{i=1}^nX_i^k=\frac{1}{n}(X_1^k+\cdots+X_n^k)$

• MM estimator $\hat \theta$ $\mu_1(\hat \theta)=M_1,\mu_2(\hat \theta)=M_2,\cdots,\mu_p(\hat \theta)=M_p$

• 需要记住的两点 $\hat \mu=M_1=\bar X\\ \hat \sigma^2 = M_2 - M_1^2=\frac{1}{n}\sum_{i=1}^nX_i^2 - \bar X^2 \\= \frac{1}{n}\sum_{i=1}^n(X_i - \bar X)^2$

• $\hat \sigma^2$的有偏性和$S^2=\frac{1}{n-1} \sum_{i=1}^n(X_i - \bar X)^2$的无偏性

Maximum Likelihood Estimation

Likelihood

• 区分：likelihood function L 和 density function f

  • 一个是参数$\theta$的函数，一个是样本x的函数

• 定义 $L(\theta)=L(\theta;X)=\prod_{i=1}^n f(X_i, \theta)\\ l(\theta)=l(\theta;X)=\log \{L(\theta;X)\}\\=\sum_{i=1}^n \log \{f(X_i, \theta)\}$

Maximum Likelihood Estimation

• 注意“截断性”的那种条件，比如要求$y\ge \theta$的话那么就要在Likelihhod的表达式中加上$I_{{(\theta,\infty)}}Y_{min}$
• Invariance property of MLEs：当出现1-1的映射$\phi=g(\theta)$的时候，则$\phi$的MLE为$\hat \phi=g(\hat \theta)$

Numerical computation of MLEs

• 目的：用迭代的方法去找到MLE

Newton-Raphson Scheme/Newton Method

• 如果只有一个参数$\theta$，那就是求二阶导，如果有多个参数的话就是求Hessian矩阵
• 初始值的确定是很重要的

The Fisher Scoring method

Differences between NM and FSM

• NM收敛更快
• 初始值对于FSM的影响更小
• 用法：一般都是先随便初始化一个初始值，用FS去找一个收敛值，然后把这个收敛值当成初始值去用NM。

Evaluating Estimation

• Note：SE只对无偏估计量有意义

Fisher Information

• If $X=(X_1,\cdots,X_n)$ and X iid $I(\theta)=I_X(\theta)=\sum_{i=1}^nI_{X_i}(\theta)=nI_{X_1}$

• 如果只有一个参数，即$\theta$是标量 $I(\theta)=E(s(\theta)^2)=-E(l''(\theta))$

Cramer-Rao Inequality

• 一个统计量（也即样本X的映射）$T=T(X)$，$g(\theta)=E(T)$，对于任意的$\theta$ $Var(T)\ge {g'(\theta)}^2/I(\theta)$

• 当无偏时，$T=T(X), g(\theta)=E(T)=\theta,g’(\theta)=1$ $MSE=Bias(T)^2+Var(T)=Var(T)\ge 1/I(\theta)$

• 这代表了无偏估计量T的精度，为其求得了一个最小值$1/I(\theta)$。此时，T为Minimum Variance Unbiased Estimator(MVUE)。

• 对于有多个参数的时候，$Var(T)-I(\theta)^{-1}$为半正定矩阵。

  

  ​

Asymptotic Properties of MLEs

• Consistency $P\{\mid\hat \theta -\theta\mid>\epsilon\}\rightarrow0$

• Asymptotic normality $\sqrt{n}(\hat \theta-\theta) \rightarrow N(0,\{I_{X_1}(\theta)\}^{-1})\\ \hat \theta \sim N(\theta, \{I_{X_1}(\theta)\}^{-1}/n)$

Exercise 6

求MLE及其性质

• 用分布的f去求likelihood function，然后取log连乘变加和，求导=0得到MLE。
• 求MLE的时候与之前一样，注意$0\le y \le \theta$截断的情况。以及有时候常数项可以不写出来。
• 得到MLE后再针对MLE去求一些相关性质比如bias，var，se甚至是分布$F(X)=P(\theta\le X)$等等。
• 分布的话，先求CDF再通过求导求pdf。

Information

• $I(\theta)=I_X(\theta)=\sum_{i=1}^nI_{X_i}(\theta)=nI_{X_1}​$，不要漏掉n啊。
• ==求E的时候的积分太太太难求了！还有就是各种公式不要记混，参数是一维还是二维都要分清楚，求的是导数还是梯度，二阶导数还是Hessian都要分清==

Chap 10 - Hypothesis Testing (I)

General setting of hypothesis test

• Notice: Not reject $\not =$ Accept
• Reject $H_0$ if $p-value\le \alpha$
• 更极端的情况是相对于$H_1$而言的

Two types of errors

The Wald test

• 前提：估计量满足渐近正态$(\hat \theta- \theta)/SE(\hat \theta)\rightarrow N(0,1)$

• 检验量：$(\hat \theta- \theta_0)/SE(\hat \theta)$

• 拒绝条件（注意单边双边

  

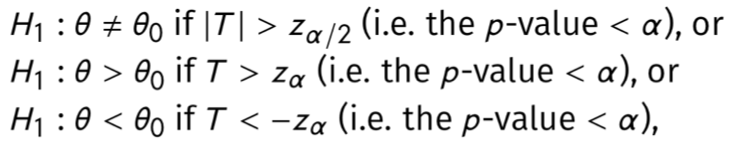
$\chi^2$ Distribution

Confidence Interval for $\sigma^2$

• 前提：$X\sim N(\mu,\sigma^2)$
• 检验量：$\sum_{i=1}^n (X_i-\bar X)^2/\sigma^2 \sim \chi^2_{n-1}$

t Distribution

An important property of normal samples

• 前提：$X \sim N(\mu,\sigma^2)$

• 已知：$\bar X=\frac{1}{n}\sum_{i=1}^nX_i,S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar X)^2,SE(\bar X)=\frac{S}{\sqrt{n}}$

• 结论：==证明==

  • $\bar X \sim N(\mu,\sigma^2/n),(n-1)S^2/\sigma^2 \sim \chi^2_{n-1}$

  • $\bar X$和$S^2$独立 $\frac{\sqrt{n}(\bar X-\mu)}{S}=\frac{\bar X-\mu}{SE(\bar X)}\sim t_{n-1}$

Accurate confidence interval for mean

看《概率论》书籍的补充【表格总结】

• t-test （one sample）
• Tests for normal means（two sample）
  • pairwise comparison - one sample t-test
  • two sample t-test
  • the wald test （也可以针对多个sample适用）

==Most Powerful Tests and Neyman-Pearson Lemma==

Exercise 7

纯构造置信区间

• 分清楚$\sigma$已知未知，用正态还是用t
• $\chi$的自由度是多少
• 一个新的统计量构造置信区间的话要先求MLE

Chap 11 - Hypothesis Testing (II)

Likelihood Ratio Tests

• 适用：当$H_0$和$H_1$都为复杂域的时候

• 检验量： $LR=\frac{\sup_{\theta\in \Theta }f(X,\theta)}{\sup_{\theta\in \Theta_0 }f(X,\theta)}=f(X,\hat \theta)/(X,\tilde \theta)$ $\hat \theta$是全局上的MLE，而$\tilde \theta$是$H_0$成立时的MLE。

• 拒绝条件：$2\log (LR) > \chi^2_k(\alpha)$

Asymptotic Distribution of Likelihood ratio test statistic

$\varphi$是我们关注的参数，而$\lambda$是我们不感兴趣（却同样未知）的参数。$k=d-d_0$，d是$\Theta$的维度，$d_0$是$\Theta_0$的维度。

The permutation test

• 目的：测验两个分布是否一样。

• 前提：无前提假设，在处理小样本的时候非常有优势。

• 核心思想：将两个样本“合”在一起看分布。

• 检验量： $T=T(X_1,\cdots,X_m,Y_1,\cdots,Y_n)\\ T=\mid\bar X-\bar Y\mid \, or \, T=\mid\bar X-\bar Y\mid^2+\mid S_x^2-S^2_y\mid$ 对于$A_{m+n}=(m+n)!$种排列都计算T，得到$T_1,\cdots,T_{(m+n)!}$

• 拒绝条件： $p=\frac{1}{(m+n)!}\sum_{j=1}^{(m+n)!}I(T_j>t_{obs}) \le \alpha\\ t_{obs}=T(X_1,\cdots,X_m,Y_1,\cdots,Y_n)$

$\chi^2$ test

Goodness of fit test

• 目的：检验样本是否服从某一给定的分布（分布已知，但参数未知）。

• 形式：列表（frequency在这里是频数而不是频率。

• 步骤：首先估计参数（利用MLE），然后计算期望频数$E_i=np_i(\hat \theta)$

  

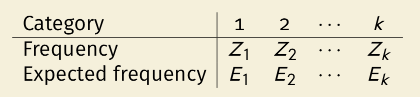
• 统计量：$T=\sum_{j=1}^k (Z_j-E_j)^2/E_j \sim \chi_{k-1-d}^2$

  d为$\theta$的维数。

• 拒绝条件：$T>\alpha$

Test for independence of two discrete random variables

• 回顾：独立性的条件为$p_{ij}=p_i p_j$

• 步骤：在$H_0$成立的条件下，$\tilde p_{ij}=\hat p_i \hat p_j = \frac{Z_i}{n} \frac{Z_j}{n}$，由此可以计算出期望频数$E_{ij}=n\tilde p_{ij}={Z_i} \frac{Z_j}{n}$

  

• 统计量：$T=\sum_{i=1}^r\sum_{j=1}^c (Z_{ij}-E_{ij})^2/E_{ij}\sim \chi^2_{p-d}$

  p为rc-1，d为r+c-2，所以$p-d=(r-1)(c-1)$

• 拒绝条件：$T>\alpha$

==Test for several binomial distributions==

Test for rxc tables - a general description

Exercise 8