ShihanRan's Blog Life is like a Markov Chain.

Artificial Intelligence

2018-03-07
Shihan Ran
Notes of Data Science Courses
 

This is a note taken in Chinese for my data science course Artificial Intelligence (DATA130008.01) in School of Data Science @Fudan University. .

Here is our class website and this is a repo including all projects and labs in my course. We use Artificial Intelligence A Modern Approach (Third Edition) as our textbook. And our course includes the following parts: Artificial Intelligence (Introduction, Intelligent Agents), Problem-solving (Solving Problems by Searching, Beyond Classical Search, Adversarial Search, Constraint Satisfaction Problems), Uncertain Knowledge and reasoning (Probabilistic Reasoning, Probabilistic Reasoning over Time, Making Simple Decisions, Making Complex Decisions), Learning (Reinforcement learning).

Introduction to Artificial Interlligence

  • Rational Decisions
    • Being rational means maximizing your expected utility
  • Tackling AI tasks
    • Real-world task —(Modeling)— Formal task —(Algorithms)— Program

Course Outline

  • Part I: Making Decisions
    • Fast search/planning
    • Constraint satisfaction
    • Adbersarial and uncertain search
  • Part II: Reasoning under Uncertainty
    • Bayes’ nets
    • Decision theory
    • Machine learning
  • Throughout: Applications
    • Natural Language, vision, robotics, games

Chapter 3. Solving problems by searching

March 7th

  • Topic: introduction to AI, uninformed search [1.0] [1.1]
  • Reading: Russell and Norvig CH1, CH2, CH3.1-3.4

March 21st

  • Topic: informed search[2.1]
  • Reading: Russell and Norvig CH3.5-3.6

Basic definition

  • 我们做出了一些假设，在这些假设下，任何问题的解都是行动的固定序列。
  • 为了达到目标，寻找这样的行动序列的过程被称为搜索。
  • Agent的简单设计为：形式化问题、搜索得到解、执行解。
  • 在表示中去除细节的过程叫抽象。
  • 搜索算法的工作就是考虑各种可能的行动序列，可能的行动序列从搜索树中根节点的初始状态出发，连线表示行动，结点对应状态空间的状态。
  • 搜索——选择一条路往下走，把其他选择暂时放在一边，等以后发现第一个问题不能求出问题的解时再考虑。
  • 图搜索和树搜索的非形式化描述：
    • 图搜索算法通过记录每个已扩展过的结点达到避免探索冗余路径的方法
    • 边缘将状态空间图分成了已探索区域和未被探索区域，每个步骤要么将一个状态从边缘变成已探索区域，要么将未探索区域变成边缘
    • 关键点：将closed set存成set而非list

Components of Search Problem

  • 状态空间
    • 初始状态、动作和转移模型一起定义了问题的状态空间
    • 即：从初始状态可以达到的所有状态的集合
  • 后继函数
    • 返回所有的后继状态
  • 初始状态
    • Agent出发时的状态
  • 目标测试
    • 确定给定的状态是不是目标状态
  • 注：书上（中文P71，英文P80）详细的说明了算法的实现以及使用的数据结构

Evaluation of Algorithm

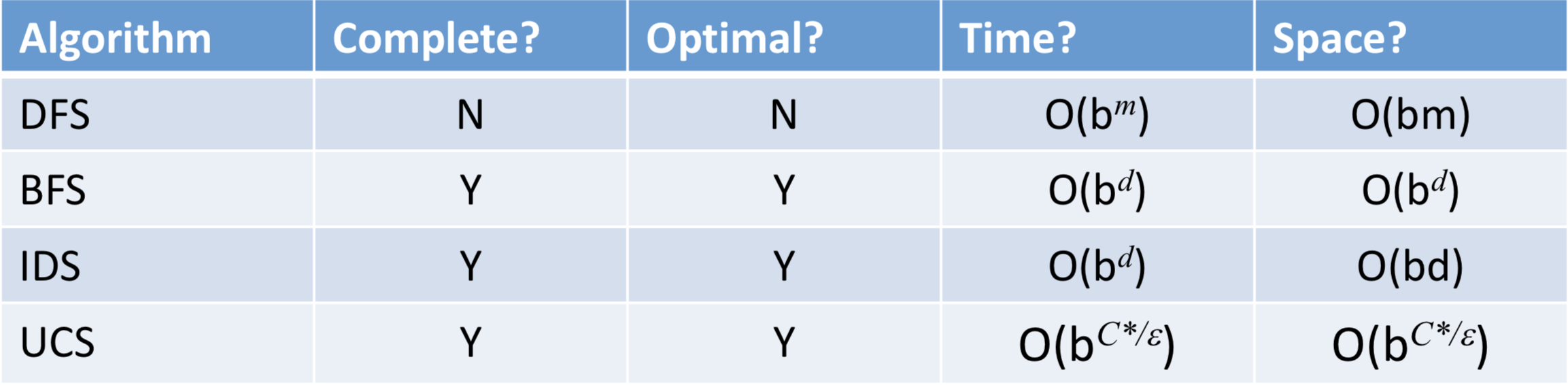
  • 完备性（能否找到解）、最优性（能否找到最优解）、空间复杂度、时间复杂度（需要多少内存 花费多长时间）
  • 复杂度依赖于状态空间中的分支因子b和最浅的解的深度d。

Uninformed Search Strategy

  • 也称为盲目搜索，意味着该搜索策略没有超出问题定义提供的状态之外的附加信息
  • 所有能做的就是生成后继结点并区分一个目标状态或一个非目标状态

Breadth First Search (BFS)

  • 算法描述：
  • 中心思想：每次总是扩展深度最浅的结点
  • 数据结构：FIFO队列
  • 完备性：总能找到最浅的目标结点，但不一定是最优的（在单位代价的情况下是最优的
  • 缺点：占空间占时间（其中内存需求是比执行时间更令人头疼的问题，具有指数级别的空间复杂度

Uniform Cost Search (UCS)

  • 算法描述：
  • 中心思想：扩展当前路径代价g(n)最小的结点，按照路径代价对队列进行排序
  • 数据结构：Priority Queue ordered by Path-Cost 优先队列
  • 完备性：完备、对于一般性的步骤代价而言算法是最优的
  • 注意：不允许有边的代价为负（否则会一直遍历这条边去使得自己的代价不断减小
  • 与BFS的显著不同：
    • 目标检测应用于结点被选择扩展时，而非结点生成的时候进行
    • 如果边缘中的结点有更好的路径到达该结点那么会引入一个测试

Deep First Search (DFS)

  • 算法描述：
  • 中心思想：每次总是扩展当前边缘结点集中最深的结点
  • 数据结构：LIFO栈
  • 完备性：
    • 有限空间中：图搜索完备（避免重复状态和冗余路径），树搜索不完备（可能会陷入死循环）
    • 无限空间中，图搜索树搜索都会失败
    • 不管是基于图搜索还是树搜索都不是最优的
  • 优点：空间复杂度（具有线性的空间复杂度，只需要存储一条从根结点到叶结点的路径及每个结点所有未被扩展的兄弟结点
  • 优化：
    • 深度受限搜索（DLS）
      • 定义：深度为l的结点被当作没有后继对待（加上了深度限制
      • 优点：解决无穷路径的问题
      • 缺点：不完备（很可能最浅的目标结点的深度超过深度限制）且不最优
    • 迭代加深的深度优先搜索(IDS)
      • （结合BFS和DFS）逐步增加深度限制反复运行直到找到目标
      • 它以深度优先搜索相同的顺序访问搜索树的结点，但先访问节点的累积顺序实际是宽度优先
      • 完备、在单位单价情况下最优
      • 时间复杂度可与BFS相比较，线性空间复杂度

双向搜索（BS）

  • 核心思想：同时进行两个搜索（一个是从初始状态向前搜索 另一个则从目标向后搜索），当两者在中间相遇时停止
  • 设计：通过一种剩余距离的启发式估计来导向
  • 降低时间复杂度
  • 不总是可行的且可能需要大量内存空间

一些总结

  • 无信息搜索策略是通过选择结点扩展的顺序来定义的
  • 指数级别复杂度的搜索问题不能用无信息的搜索算法求解，除非是规模很小的实例

Informed Search Startegy

  • 可以采用超出问题本身定义的、问题特有的知识，因此能够找到比无信息搜索更有效的解
  • 中心思想：结点是基于评估函数$f(n)$的值被选择扩展的
    • 评估函数被看作是代价估计，评估值最低的结点被选择首先进行扩展
  • 评估函数$f(n)$：由启发函数$h(n)$构成，用于选择一个结点进行扩展
  • 启发函数$h(n)=$结点$n$到目标结点的最小代价路径的代价估计值
    • 以结点为输入，但只依赖于结点状态
    • 若$n$是目标结点，则$h(n)=0$
  • 代码实现：算法结构与UCS一致，根据$f$值对优先队列排序
  • 中心思想：试图扩展离目标最近的结点，认为这样可能可以很快找到解
  • 只采用启发式信息：$f(n)=h(n)$
  • 贪婪的定义：在每一步都要试图找到离目标最近的结点
  • 完备性：效率较高，不完备，且不一定能保证最优性（取决于特定的问题和启发式函数的质量
  • 中心思想：对结点的评估结合了到达此结点已经花费的代价$g(n)$和从该结点到目标结点所花代价$h(n)$，即$f(n)=g(n)+h(n)$，扩展$f(n)$最小的结点
  • 评估函数：$f(n)=$经过结点n的最小代价解的估计代价（整体消耗）
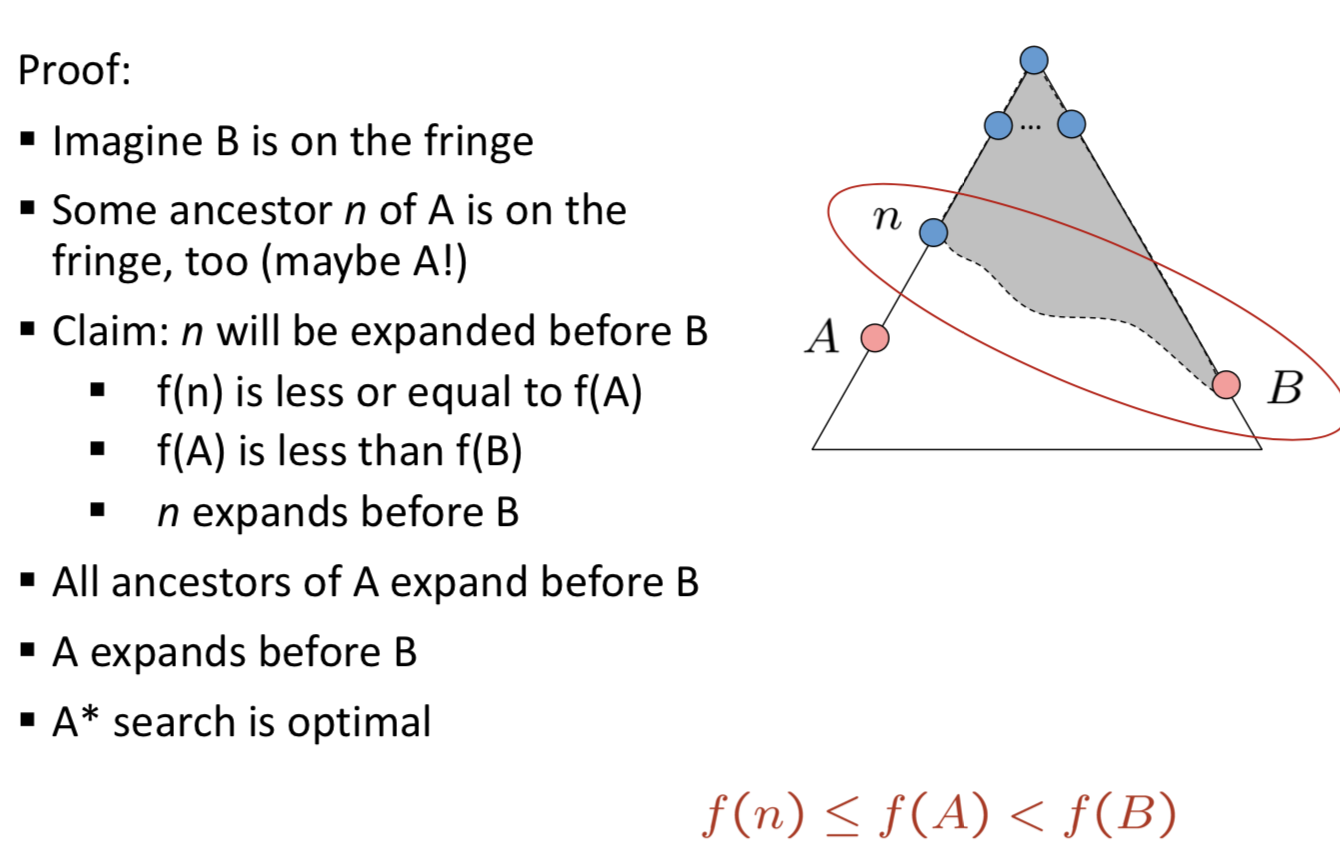
  • 完备性：如果$h(n)$可采纳（对于树搜索而言）或是一致的（对于图搜索而言），则A*算法完备且最优
    • 可采纳性
      • 定义：指不会过高估计到达目标的代价
      • 结论：$f(n)$不会超过经过结点$n$的解的实际代价
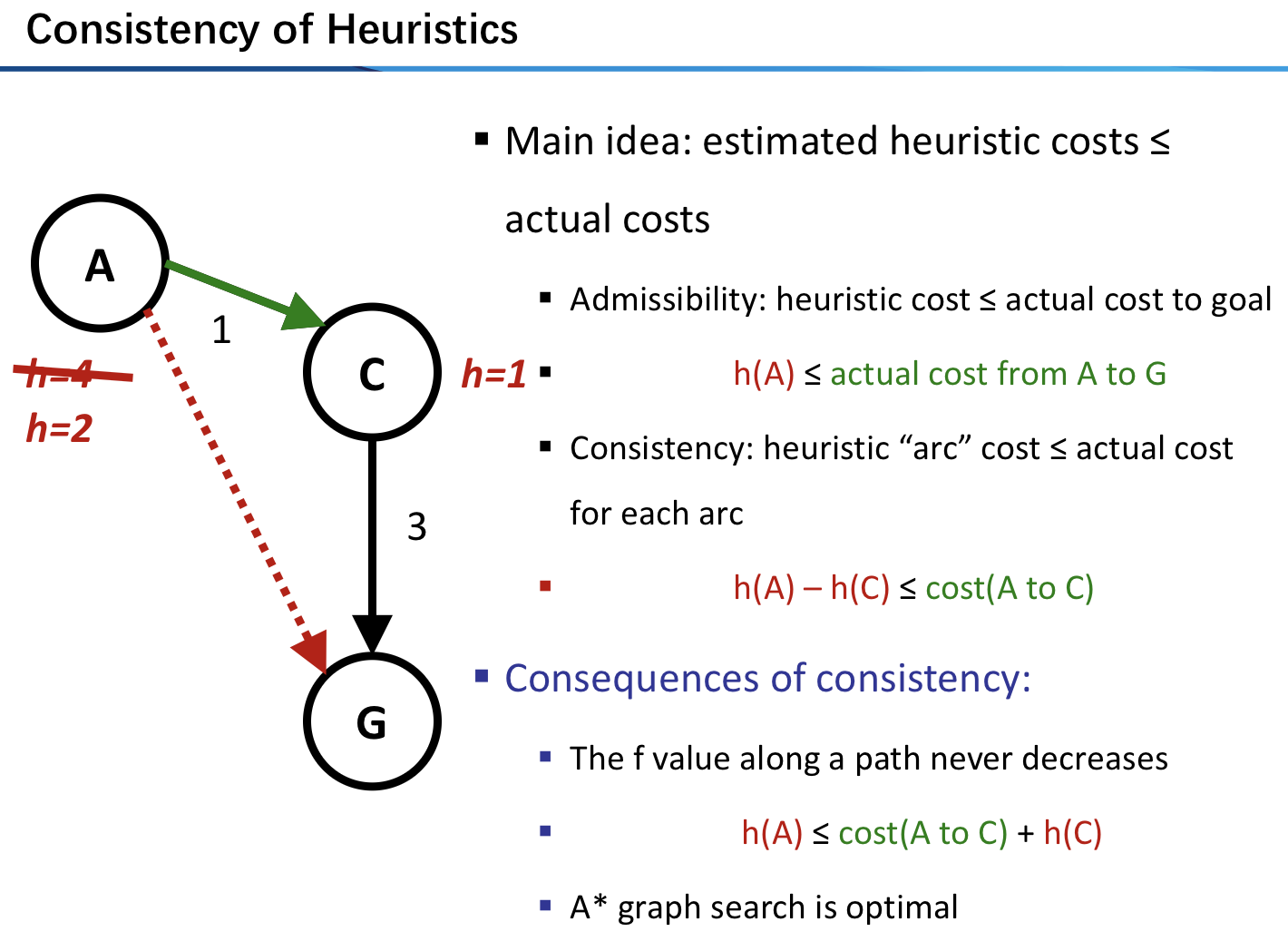
    • 一致性（条件比可采纳性更强
      • 定义：对于每个结点$n$和通过任一行动$a$生成的$n$的每个后继结点$n’$，从结点$n$到达目标的估计代价不大于从$n$到$n’$的单步代价与从$n’$到达目标的估计代价之和：$h(n)\le c(n,a,n’)+h(n’)$
      • 结论：一致的启发式都是可采纳的
    • 可采纳性与一致性：
    • ==证明！==
  • 缺点：空间复杂度很高

Heuristic

  • 启发式搜索算法的性能取决于启发式函数的质量

  • 刻画启发式：有效分支因子$b*$

    • 如果$A^$算法生成的总结点数为N，解的深度为d，那么$b^$就是深度为d的标准搜索树为了能够包括N+1个结点所必需的分支因子，即：

    • 良好的启发式会使$b*$的值接近于1

  • 对于任意结点n，$h_2(n)\ge h_1(n)$，称$h_2$比$h_1$占优势

    • 一般来说使用值更大的启发式函数是好的，前提是计算该启发式花费的时间不是太多的话（Trade off
    • 因为每个$f(n)<C^$的结点都将被扩展，也即：$h(n)<C^-g(n)$的结点一定会被扩展

从松弛问题出发设计可采纳的启发式

  • 松弛问题：减少了行动限制的问题成为松弛问题
  • 注意：松弛问题增加了状态空间的边，所以原有问题中的任一最优解同样是松弛问题的最优解，但由于增加的边可能导致捷径所以松弛问题可能存在更好的解
  • 选择启发式：$h(n)=\max {h_1(n),\cdots,h_m(n)}$

从子问题出发设计可采纳的启发式：模式数据库

  • 模式数据库：对每个可能的子问题实例存储解代价
    • 这些启发式可以像前面所讲的那样取最大值的方式组合使用
  • 改进：不相交的模式数据库

动态规划

从经验中学习启发式

  • 经验：求解大量的该问题，把每次的最优解都成为学习实例，每个实例包括解路径上的一个状态和从这个状态到达解的代价

Chapter 5. Adversarial search

April 4th

  • Topic: adversarial game, utility [3.1] [3.2]
  • Reading: Russell and Norvig CH5

Optimal Decisions in Games

Basic Definition

  • 博弈的定义：有完整信息的、确定性的、轮流行动的、两个游戏者的零和游戏
    • 在确定的、完全可观察的环境中两个Agent必须轮流行动，在游戏结束时效用值总是相等并且符号相反
    • Agent之间效用函数的对立导致了环境的对抗
  • 博弈的表示
    • 初始状态（棋盘设置）
    • 每个状态下的合法行动
    • 每个行动的结果
    • 终止测试（说明什么时候游戏结束）
    • 终止状态上的效用函数

MiniMax and Alpha-Beta Pruning

  • 极小极大算法可以通过对博弈树的深度优先枚举选出最优招数
    • 与DFS类似 时间复杂度：$O(b^m)$ 空间复杂度：$O(bm)$
    • 提高效率：截断搜索、$\alpha$-$\beta$剪枝算法
  • $\alpha$-$\beta$剪枝算法可以计算出和极小极大算法一样的最优招数，由于消除了被证明无关的子树所以提高了效率
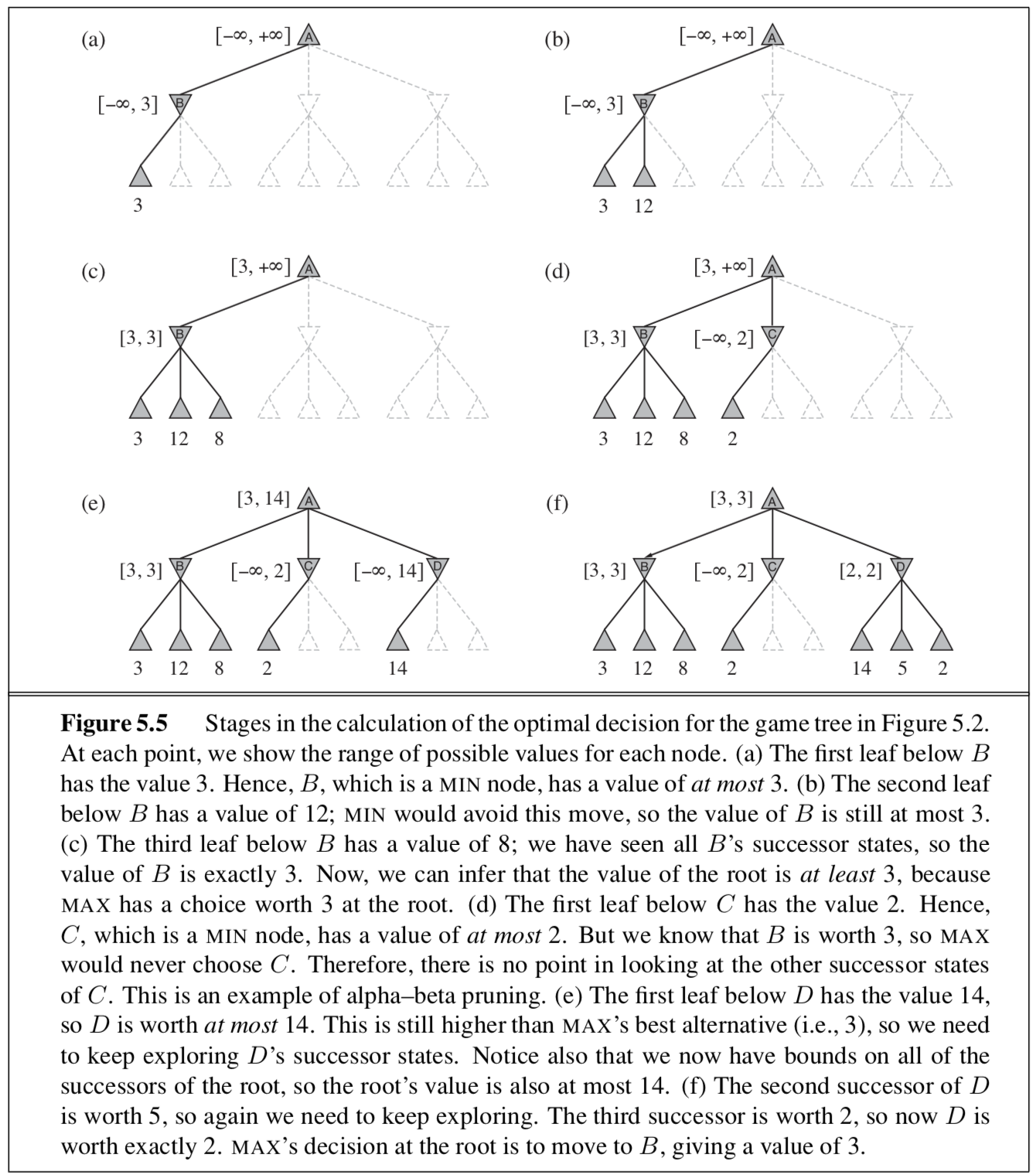
    • Max结点只改变alpha，Min结点只改变beta
  • 在某个点截断搜索并应用评估函数对某个状态的效用值进行计算的方法可以极大提高效率（由于评估函数的近似本质，该算法不一定能保证准确性
    • 评估函数的缺点：近似、树越深评估函数越差、计算评估函数的时间是一个tradeoff
  • 很多博弈程序会提前计算好表，通过查表而非搜索来计算最佳招数
  • 扩展：多人博弈
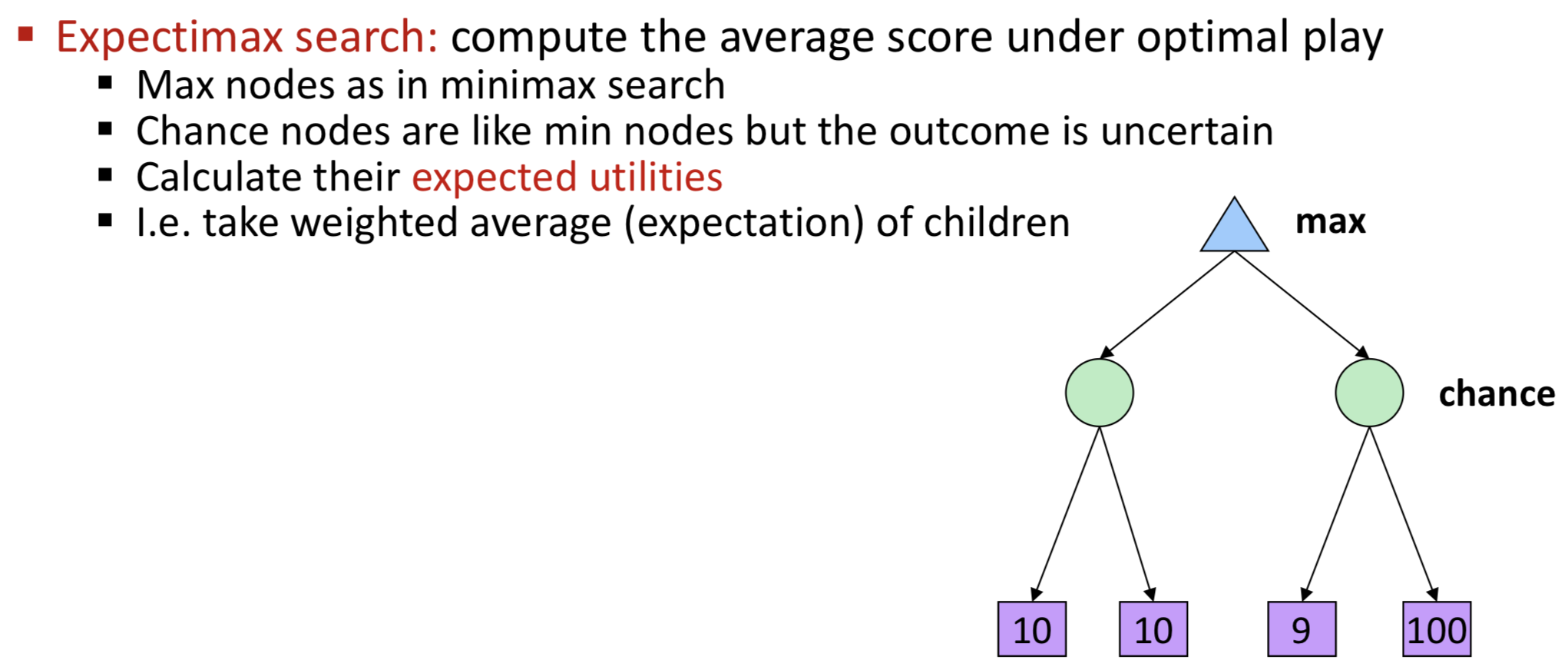
  • 机会博弈可以通过扩展极小极大算法来求解，扩展后的算法通过计算其全部子结点的平均效用值来评价机会结点
    • 全部子结点都需要考虑到！
    • 机会结点取代了之前的min结点 Chance nodes are like min nodes but the outcome is uncertain

Utilities

  • 定义：functions from outcomes (states of the world) to real numbers that describe an agent’s preferences【本质：映射】

  • MEU（最大期望效用）

    • 理性的Agent应该选择能够最大化Agent期望效用的行为

  • 偏好关系的几个约束：

  • MEU定理

Chapter 16. Making Simple Decisions

April 4th

  • Topic: adversarial game, utility [3.1] [3.2]
  • Reading: Russell and Norvig CH16.1-16.3

Chapter 4. Beyond Classical Search

April 18th

  • Topic: constraints satisfactory problems, local search [4.1]
  • Reading: Russell and Norvig CH4.1-4.2

Chapter 6. Constraint Satisfaction Problems

April 18th

  • Topic: constraints satisfactory problems, local search [4.1]
  • Reading: Russell and Norvig CH6

Basic Introduction

What is CSPs

  • 其状态必须满足若干约束和限制的一组对象
  • 将问题中的实体表示为对变量进行有限约束的同质集合，通过约束满足方法加以解决。

Standard Search Problem vs. Constraint Satisfaction Problem

  Standard Search Problem Constraint Satisfaction Problem
State 其状态是原子的或不可分割的 状态采用一系列变量表示，每个有相应的值
Heuristics problem-specific general-purpose heuristics
Do what? Only Search Search and constraint propagation （采用约束来减少一个变量的合法值的数量，相应地可以减少其他变量的合法值

Formal Definition of CSP

$<X,D,C>$  
$X$ a set of variables, ${X_1, \dots, X_n}$
$D$ a set of domains, ${D_1,\dots, D_n}$. One $D_i$ for each variable $X_i$ ,consisting of a set of values ${V_1, \dots, V_k}$
C a set of constrains, ${C_1,\dots, C_m}$. Each $C_i$ consists of a pair $<scope, rel>$, where, scope is a tuple of variables that participate in the constraint, rel is a relation that defines the values that those variables can take on.
State Space and the notion of a solution Each state is defined by assignment of values to variables: ${X_i = v_i, X_j = v_j , \dots}$

Solving CSPs

Constraint propagation

Different types of local consistency

  • 节点一致性
    • 变量的Domain中的所有值满足变量的一元约束
  • 弧一致性
    • 变量的Domain中的所有值满足变量的二元约束
    • Note：最流行的约束传播方法是AC-3算法，它支持弧一致性
  • 路径一致性
    • 对于与${X_i, X_j}$约束一致的每个赋值${X_i = a, X_j = b}$，如果存在一个满足对${X_i, X_m}$和${X_m, X_j}$ 约束的$X_m$赋值，则二元变量集${X_i, X_j}$对于第三个变量$X_m$是路径一致的。
  • k一致性
    • 对于任意$k - 1$个变量的集合以及对于这些变量的任意一致性赋值，如果某个一致性值总是能够被赋值于任意第k个变量，则该CSP是k一致性的。

Introduction

  • 深度优先搜索的通用算法
  • 回溯搜索递增地构建解的候选，一旦确定$c$不能成为一个解则将$c$抛弃（回溯）

  • 例子：

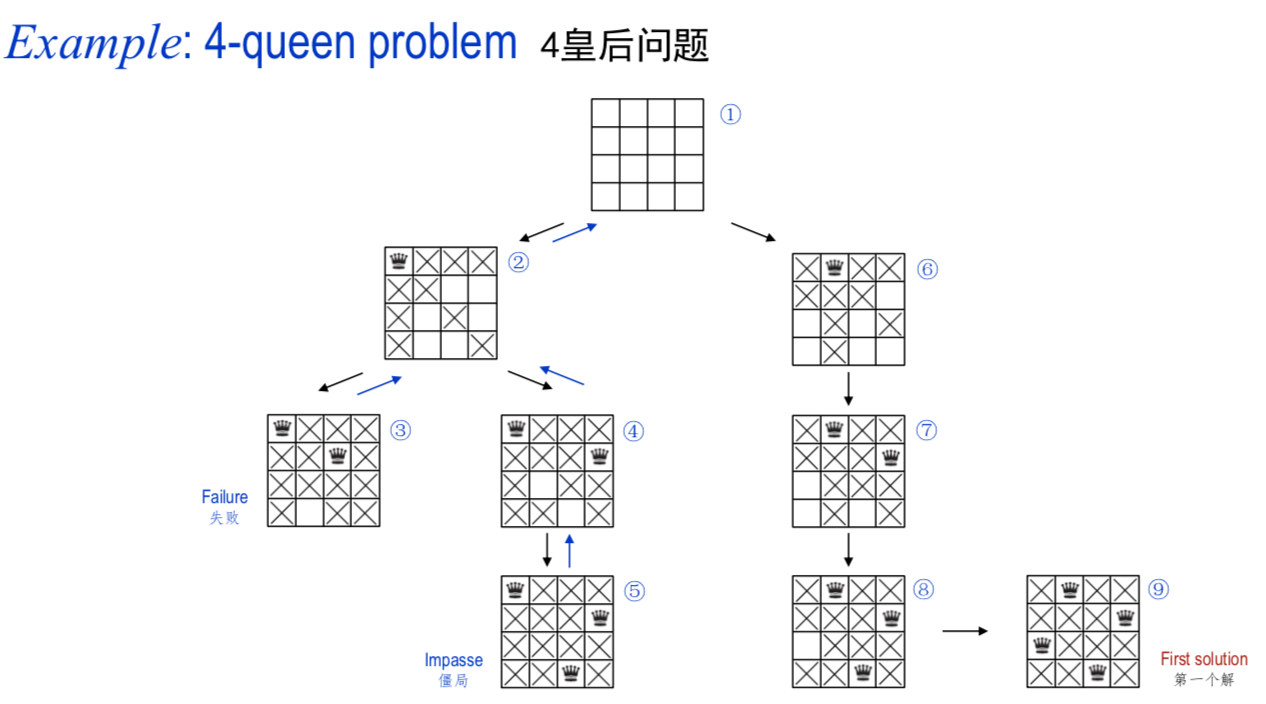
  • 算法：

Improving Backtracking

  • 改善回溯的若干问题：
The heuristic strategies of Ordering
  • Minimum-remaining-values or Most constrained variable (MRV or MCV)
    • 选择具有最少“合法”值的变量
  • Degree heuristic
    • 选择参与其他未分配变量的最大约束数来减少未来选择的分支因子
  • Least-constraining-value heuristic
    • 选取能排除约束图中相邻变量最少选择的值
  • 前向检查推理在搜索中会很有用
  • 例子：
Intelligent Backtracking

  • 回到先前的变量并尝试不同的值

  • Structure

    • 找到独立子问题
    • Tree-Structured CSPs
      • 第一步：从下往上（从叶子结点开始往根结点）做弧相融检查
        • 树结构中 叶子结点做了之后就不会变了 不需要回溯 ：）
      • 第二步：从根结点到叶子结点的一个赋值
    • Nearly Tree-Structured CSPs

Local search for CSPs

  • 采用完整状态形式化
    • 初始状态：为每个变量赋值
    • 搜索：一次改变一个变量的值
  • 例子：

Min-conflicts Heuristic

  • Features
    • 变量选择：随机选择任意一个冲突变量
    • 值的选择：选择导致与其它变量呈现最少冲突的新值
  • 算法：
  • 注意：
    • 初始状态可以随机选择，依次为每个变量选择一个最小冲突值。
    • 给定当前赋值的其余部分，CONFLICTS函数计算特定值违反约束的个数。

Constraint Weighting

  • 想法：能够聚焦于重要的约束条件
  • 益处
    • 对高原增加了地势，确保能够改善当前的状态。
    • 对证明难以求解的约束也增加权重。

The Structure of Problems

Decomposing Problem

  • 背景
    • 现实世界的问题可以被分解为许多子问题
    • 由约束图所表征的问题结构，可以用于寻找解。

Independent Sub-problems

  • 独立子问题可被标识为约束图的联结组件
  • 不分解，总的运行是$O(d^n)$
  • 分解后，设n个变量的图可分解为仅有c个变量的子问题：每个最坏解的代价是$O((n/c)\cdot d^c)$，n的线性关系

Tree-structured Problems

  • 任何树结构的CSP可以在变量数的线形时间解决
  • 求解树结构CSP的方法：先挑选任意变量作为树的根，然后再选择一个排列(称为拓扑排序)
  • 例子：
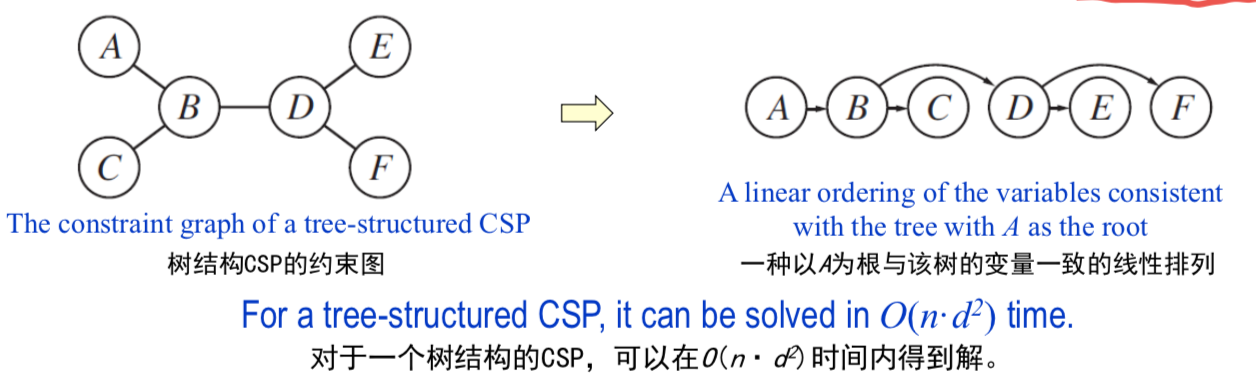
  • 算法：

Reduce Constraint Graphs to Tree Structures

  • 1st approach: cutset conditioning
    • 将一个通用CSP问题简化为一个树结构CSP，并且若能够找到一个小割集则相当有效
    • Conditioning：对一个变量进行实例化，剪去它的相邻范畴
    • 例子和时间复杂度分析：
  • 2nd approach: tree decomposition
    • 将CSP转换成一棵子问题树，并且当该约束图的树宽较小时很有效
    • 例子和时间复杂度分析：

Chapter 17. Markov Complex Decisions

April 25th

  • Topic: Markov Decision Process [5.1] [5.2]
  • Reading: Russell and Norvig CH17.1-17.3
  • Goal: Maximize sum of rewards

Basic Definition

  • An MDP is defined by
    • A set of states $s\in S$
    • A set of actions $a\in A$
    • A transition function T(s, a, s’)
      • Probability that a from s leads to s’, i.e., $P(s’\mid s, a)$
      • Also called the model or the dynamics
    • A reward function R(s, a, s’)
      • Sometimes just R(s) or R(s’)
    • A start state
    • Maybe a terminal state
  • Policies
    • For MDPs, we want an optimal policy $\pi$*: mapping (S → A)
    • $\pi(s)$表示策略为状态s所推荐的行动a
  • Utilities and discounting
    • 衰减因子$\gamma$ （拿到手的才是最好的
    • 解决无穷大效用值->
  • Stationary Preference

Chapter 21. Reinforcement Learning

May 2nd

  • Topic: Reinforcement Learning [6.1]
  • Reading: Russell and Norvig CH21.1-21.4

Basic Definition

  • Still assume a Markov decision process (MDP):
    • A set of states s $\in$ S
    • A set of actions (per state) A
    • A model T(s,a,s’)
    • A reward function R(s,a,s’)
  • Still looking for a policy $\pi(s)$
  • Model-Based Idea:
    • Learn an approximate model based on experiences
    • Solve for values as if the learned model were correct
    • 去学状态转移函数和回报函数

Chapter 15. Probabilistic Reasoning over Time

May 16th

  • Topic: Hidden Markov Model [7.0] [7.1] [7.2]
  • Reading: Russell and Norvig CH15.1-15.5
  • 转移模型：描述给定过去时刻的世界状态，在时刻t变量的概率分布。
  • 传感器模型：描述给定当前世界状态，在时刻t每个感知的概率分布。

15.1 Time And Uncertainty 时间与不确定性

我们已经发展了在静态世界进行概率推理的技术，仍需要研究动态世界的概率推理问题。

状态与观察

将世界看做一个时间片(time slice)，在时刻t，不可观察的状态变量集是$X_t$，可观察的证据变量集是$E_t$。

转移模型与传感器模型

  • 探究的问题：世界如何演变(转移模型)，证据变量如何获得它们的取值(传感器模型)。

  • 马尔科夫假设(Markov Assumption)：当前状态只依赖于有限的固定数量的过去状态，该过程被称为马尔科夫过程(Markov Process)或马尔科夫链(Markov chain)。n阶马尔科夫过程即：

  • 稳态过程：变化过程本身不随时间变化的规律支配。 静态过程：状态本身不发生变化。

  • 传感器马尔科夫假设：$P(E_t X_{0:t}, E_{0:t-1})=P(E_t X_t)$
  • 传感器模型(观察模型)：$P(E_t X_t)$
    转移模型:$P(X_t X_{t-1})$

  • 通过时刻0的先验概率分布$P(X_0)$，我们可以确定完全联合概率分布：

  • 两种方法提高近似的精确程度

    • 提高马尔可夫过程模型的阶数
    • 扩大状态变量集合
    • 注意
      • 提阶数总能通过扩大状态变量集合重新进行形式化而保持结束不变
      • 增加状态变量虽然可能会提高系统的预测能力但同时也增加了预测的要求：这些新变量也是必须要预测的

15.2 Inference in Temporal Models 时序模型中的推理

滤波和预测

滤波

给定目前为止所有证据，计算当前状态的后验概率分布。滤波也称为状态估计(state estimation)，即$P(X_{t+1} e_{1:t})\rightarrow P(X_{t+1} e_{1:t+1})$的递归估计：
  • 理解：$P(X_t e_{1:t})$是沿着序列前向传播的“消息”$f_{1:t}$，它在每次转移时得到修正，并根据新的证据进行更新，过程为：$f_{1:t+1}=\alpha \text{FORWARD}(f_{1:t}, e_{t+1})$
  • 在这个求和表达式中，第一个因子$P(X_{t+1} x_t)$来自转移概率，第二个因子$P(x_t e_{1:t})$来自当前状态分布。

预测

  • 给定到目前为止的所有证据，计算未来状态的后验分布。也就是对于某个$k>0$计算$P(X_{t+k} e_{1:t})$，即无新证据的前向滤波，用条件化概率推理即可：
    • 拓展1：证据不变，预测未来的概率世界会达到稳态，$P(X_{t+k+1}|e_{1:t})$达到稳态分布(stationary distribution)的时间被称为混合时间(mixing time)。 转移模型中不确定性越大，混合时间越短，未来越模糊。
    • 拓展2：通过前向递归求证据序列的似然$P(e_{1:t})=\sum_{x_t}P(x_t,e_{1:t})$会发现，当时间流逝，这个概率数值上越来越小。

平滑

  • 平滑：给定目前为止的所有证据，计算过去某一状态的后验概率。即$P(X_t e_{1:t})\rightarrow P(X_k e_{1:t})$，且$k<t$。
  • 理解：其中前向消息$f_{1:k}$通过前向滤波过程计算，后向消息$b_{k+1:t}$通过一个从$t$开始向后递归过程来计算，概率推理技术是条件化和条件独立性(马尔科夫覆盖)，这里$b_{t+1:t}=P(e_{t+1:t} X_t)=P( X_t)=1$。：
  • 前向-后向算法(forward-backward algorithm)：通过动态规划对前向过程进行记忆化，将整个序列的平滑复杂度降低到$O(t)$。

寻找最可能解释

  • 最可能解释：给定观察序列，找到最可能生成这些观察结果的状态序列。

  • 猜想1：平滑贪心，每次用平化算法中单步$t$中最有可能的后验分布去生成猜想的天气$r_t$。但该方法没有考虑到所有时间步中的联合概率最优，所以与真实结果可能有极大差距。

  • 猜想2：因为马尔科夫假设，所以到达$t$的最可能路径中包含了到达$t-1$的最可能路径，所以对于前向过程$f_{1:t+1}=\alpha \text{FORWARD}(f_{1:t}, e_{t+1})$： 该算法的复杂度为$O(t)$，被称为Viterbi算法。

15.3 Hidden Markov Models 隐马尔可夫模型

  • 定义：单个离散随机变量描述状态过程的时序概率模型。
  • 推论：多个变量可以通过元组组合成一个大的单变量，使其仍符合马尔科夫模型。

简化的矩阵算法

  • 转移模型的矩阵表示：$S\times S$的矩阵$T$，其中$T_{ij}=P(X_t=j X_{t-1}=i)$。
  • 传感器模型的矩阵表示：$S\times S$的矩阵$O_i=P(e_t X_t=i)$，非对角元素为0。
  • 前向公式： $f_{1:t+1}=\alpha O_{t+1}T^Tf_{1:t}$。
  • 后向公式：$b_{k+1:t}=TO_{k+1}b_{k+2:t}$。
  • ==联机平滑：存在一种时间复杂度和延迟长度无关的算法。==

隐马尔科夫模型实例：定位

15.4 Kalman Filters 卡尔曼滤波器

  • 任务 ：根据随时间变化且带有噪声的观察数据去估计连续的状态变量。
  • 假设： 转移模型和传感器模型是线性高斯模型。转移模型为：

更新高斯分布

  • 特性： 卡尔曼滤波的$\text{FORWARD}$算子选取一个高斯前向消息，该消息由均值$\mu_t$和协方差$\Sigma_t$确定；并产生一个新的多元高斯前向消息$f_{1:t+1}$，该消息由均值$\mu_{t+1}$和协方差矩阵$\Sigma_{t+1}$确定。
  • 结论：用一个线性高斯模型进行滤波，任何时间片都会产生一个高斯状态分布。

一个简单一维实例

一般情况

15.5 Dynamic Bayesian Networks 动态贝叶斯网络

  • 动态贝叶斯网络的多个状态变量和证据变量可以合在一起变成隐马尔科夫模型的单个变量。

  • 理解：可以说DBN之于HMM，相当于贝叶斯网络之于完全联合分布。

构造动态贝叶斯网络

  • 三类信息：状态变量的先验分布$P(X_0)$，转移模型$P(X_{t+1} X_t)$，传感器模型$P(E_t X_t)$。
  • 一种结构：状态变量和证据变量之间连接关系的拓扑结构，且这种结构相对于每一个时间片都是相同的，称为稳态。
  • 瞬时故障、持续故障建模。

动态贝叶斯网络的精确推理

  • 摊开(unrolling)： 通过展开贝叶斯网络，获得全贝叶斯网络，使用14章中的变量消元、聚类算法等求解。但时空复杂度比较高。
  • 我们可以只保存$t$和$t+1$的时间片变量集，但每次更新所需要的“常数”时间和空间复杂度是状态变量个数的指数级。

动态贝叶斯网络的近似推理

  • 粒子滤波算法

    1. 对于每个样本，通过转移模型$P(X_{t+1} x_t)$，在给定样本当前状态值$x_t$条件下，对下一个状态值$x_{t+1}$进行采样，使得该样本前向传播。
    2. 对于每个样本，用它赋予新证据的似然值$P(e_{t+1} x_{t+1})$作为权值。
    3. 对于总体样本进行重新采样，以生成一个新的$N$样本总体。每个新样本是从当前的总体中选取的；某个特定样本被选中的概率与其权值成正比，新样本没有赋予权值。

15.7 Summary 本章小结

  • 世界中变化的状态是通过用一个随机变量集表示每个时间点的状态来处理的。
  • 可以把表示方法设计成满足马尔可夫特性，这样给定当前状态后，未来就不再依赖于过去。再结合稳态过程假设——也就是说，过程的动态特性不随时间发生改变——这样能够大大简化对问题的表示。
  • 可以认为时序概率模型包含了描述状态演变的转移模型和描述观察过程的传感器模型。
  • 时序模型中的主要推理任务是：滤波、预测、平滑以及计算最可能解释。其中每一个任务都可以通过简单的递归算法实现，其运行时间与序列长度呈线性关系。
  • 更深入地研究了时序模型的3个家族：隐马尔可夫模型，卡尔曼滤波器，以及动态贝叶斯网络（前两者是后者的特殊情况）。
  • 如果不像卡尔曼滤波器一样做特殊假设，具有许多状态变量的精确推理是不可操作的。实践中，粒子滤波算法似乎是一种有效的近似算法。

Chapter 14. Probabilistic Reasoning

May 23rd

Goal

  • 用贝叶斯网络(Bayesian Networks)的形式系统性地描述世界的概率，然后说明如何高效地进行推理(inference)。

14.1 不确定性问题域中的知识表示

贝叶斯网络表示变量之间的依赖关系，本质上可以表示任何完全联合概率分布，在很多情况下这种表示是简明扼要的。贝叶斯网络是一个有向无环图(DAG)，其完整说明如下：

  • 每个结点对应一个随机变量，变量可以是连续的或者离散的。
  • 一组有向边连接结点对，若有结点$X$指向结点$Y$，称$X$是$Y$的一个父节点(parent)。
  • 每个结点$X_i$有一个条件概率分布$P(X_i Parents(X_i))$，量化其父结点对该结点的影响。

14.2 贝叶斯网络的语义

两种理解方式

  • 视为对联合概率分布的表示 —> 帮助理解如何构造网络。
  • 视为对一组条件依赖性语句的编码 —> 帮助设计推理过程。

表示完全联合概率分布

  • 联合分布中的一般条目是对每个变量赋一个特定值的合取概率，比如$P(X_1=x_1 \wedge x_2 \wedge … \wedge x_n )=\prod_{i=1}^nP(x_i parents(X_i))$。

==一种构造贝叶斯网络的方法==

  • 链式规则：

  • 则对于$Parents(X)\subseteq {X_{i-1},…,X_i}$:

  • 当给定父结点之后，每个结点条件独立于结点排序顺序中其他祖先结点时，贝叶斯网络是问题域的正确表示。构造方式可以如下：
    • 结点(Nodes): 任何排序都可，但如果原因排在结果之前，则网络更加紧致。
    • 边(Links): i从1到n，执行：
      • 从$X_1, …,X_{i-1}$中选择$X_i$的父结点的最小集合，使得上述公式得到满足。
      • 在每个父结点与$X_i$间插入一条边。
      • 条件概率表(CPTs)：写出条件概率表$P(X_i Parents(X_i))$
  • 贝叶斯网络的特性：
    • 每个结点只与排在它前面的结点相连，保证构造出的网络是无环的。
    • 网络中没有冗余的概率值，因此不会出现不一致。

紧致性与结点排序：

  • 贝叶斯网络至多用到$n2^k$个值描述，而完全联合概率分布将包含$2^n$个数值。$k$通常是一个比较小的常数。
  • 但是糟糕的变量排序，会影响网络的紧致性

贝叶斯网络中条件独立关系

给定贝叶斯网络网络的父结点、子结点、子结点的父结点，即马尔科夫覆盖(Markov Blanket)。==为什么不是只包括父结点呢？==

14.3 条件分布的有效表示

  • 确定性结点(deterministic nodes): 一个确定性结点的取值完全由其父节点取值决定。
  • 噪声(noisy): 噪声或(Noisy-OR)和遗漏结点(leak node)

包含连续变量的贝叶斯网络：

  • 离散化(discretization): 回避连续变量。
  • 参数指定(parametric)
  • 非参数化(nonparametric)

混合贝叶斯网络(hybrid Bayesian Network):

  • 给定离散或连续父结点下的连续随机变量条件分布。
    • 线性高斯分布(linear Gaussian Distribution)：
      • 均值$\mu$随着父结点的值线性变化
      • 标准差$\sigma$保持不变。
    • 条件高斯分布(conditional Gaussian):
      • 给定全部离散变量任意赋值，所有连续变量的概率分布是多元高斯分布。
  • 给定连续父结点下离散随机变量的条件分布。
    • 概率单位分布(probit distribution)，和**逻辑单位分布(logit distribution)。

14.4 贝叶斯网络中的精确推理

概率推理系统的基本任务：

  • 给定某个观察事件(event)，也就是证据变量(evidence variables)之后，计算一组查询变量(query variables)的后验概率分布，即$P(X\mid e)$。非证据非查询变量称为隐藏变量(hidden variable)。
  • 精确推理基本是不可操作的。

通过枚举进行推理

  • 复杂度：$O(n2^n)\rightarrow O(2^n)$
  • Enumeration-ask 算法通过深度优先递归表达树进行求值。

变量消元算法

对所有复杂计算只进行一次计算，动态规划。

精确推理的复杂度

单连通网络(singly connected)或多形树(polytree)，精确推理的时间和空间复杂度与网络规模呈线性关系，这里的网络规模指CPT表的条目数。

多连通网络(multiply connected)变量消元算法具有指数级时空复杂度，贝叶斯网络推理是NP难的。

聚类算法

聚类算法(clustering algorithm)也称为联合树算法(join tree algorithm)，时间可以减少到$O(n)$。

14.5 贝叶斯网络中的近似推理

14.8 本章小结

  • 贝叶斯网络是一种成熟的不确定知识的表示方法。它是一个有项无环图，结点对应于随机变量；每个结点都有一个给定父节点下的条件概率分布。
  • 贝叶斯网络提供了一种表示问题域中的条件独立性关系的简洁方式。
  • 贝叶斯网络指定了全联合概率分布；其中每个联合条目定义为局部条件分布中的对应条目的乘积。贝叶斯网络的规模往往指数级地小于全联合概率分布。
  • 很多条件分布都可以用规范分布族紧凑地表示出来，同时包含离散随机变量和连续随机变量的混合贝叶斯网络使用各种规范分布。
  • 贝叶斯网络中的推理意味着给定一个证据变量集合后，计算一个查询变量集合的概率分布。精确推理算法，比如变量消元算法，尽可能高效地计算条件概率的乘积之和。
  • 在多形树(单连通网络)中，精确推理需要花费的时间与网络规模呈线性关系，而在其他一般情况下，精确推理是不可操作的。
  • 像似然加权、MCMC方法这样的随机近似技术能够提供对网络的真实后验概率的合理估计，并能够比精确算法处理规模大得多的网络。

Similar Posts

Previous Pytorch tutorial

Next Data Visualization

Comments

Content