This is a note taken in Chinese for my data science course Social Network Mining.
We use this as our textbook. And our course includes the following parts: Introduction, Essentials (Graph Essentials, Network Measures, Network Models, Data Mining Essentials), Communities and Interactions (Community Analysis, Information Diffusion in Social Media), Applications (Influence and Homophily, Recommendation in Social Media, Behavior Analytics).
Introduction(书上没有!)
- 社交网络分析的意义:应从社会的角度去分析和理解个人的行为
Introduction to Social Network
Definition of Social Network
- 由特定集合的行动者(点)以及行动者之间的关系(线)组成(图),包括行动者、关系、联结三个基本概念
- 行动者:个人、团队或组织
- 类型:桥/联络人/孤独者/明星/结构洞
- 关系:友谊、师生、同事等,可存在方向和强弱甚至正反
- 联结:两个行动者形成关系时必须通过某种直接或间接途径建立彼此的联结
- 行动者:个人、团队或组织
History of Social Network
- 六度空间=六度分隔=小世界理论
- 150定律:邓巴数字,拥有稳定社交网络的人数
Social Network Analysis
- 技术基础:图论和社会计量学
- 特点
- 源自于联系社会行动者关系基础之上的结构性思想
- 以系统的经验数据为基础
- 非常重视关系图形的绘制
- 依赖于数学或计算模型的使用
- 分类
- 自我中心网络
- 从研究的个体出发,研究其与直接或间接的联结,找出由中心向外扩展的关系网络。
- 整体社会网络
- 主要研究网络结构问题。
- 自我中心网络
社会计算
- 定义
- 利用计算系统帮助人们进行沟通与协作
- 利用计算技术研究社会运行的规律与发展趋势
- 应用
- 舆情分析、社区发现、人际关系挖掘等
- 挑战
- 数据清理与噪音消除
- 性能/作用评价
- 数据分析/挖掘的结果往往能较好的解释what/where/when/how many/how often 但较难回答why
图论基础
基本结构
- 图的符号表示:G(V,E)
- 结点/节点(vertex/node)
- 边(edge)
- 注意:有向图中,结点邻居有入度和出度之分
- 边的重数:平行边的条数
- n阶图:图的结点的个数
- 度:与一个结点相连接的边数
- 注意:有向图中,出度入度可以想成一个人的关注数和粉丝数
- 度数为1的结点是悬挂结点,度数为0的为孤立点
- ==相关定理:==
- 无向图中所有结点的度数之和是边数的2倍
- 无向图中度数为奇数的结点数有偶数个
- 有向图中所有结点的入度之和等于所有结点的出度之和
- 度分布:P(d)代表随机选择的结点v的度数为d的概率
- 幂律分布:大多数用户有很少的朋友,较少的用户有很多的朋友。
- 网络图的密度:实际边数与理论上最大的边数之比
- 无向图:$\frac{L}{n(n-1)/2}$
- 有向图:$\frac{L}{n(n-1)}$
表示
- 表示方法
- 邻接矩阵/邻接表/边列表
- 图同构
- 定义 - 如果把其中一个图中的结点重新排列,边跟着结点移动,并且可以任意弯曲,能够与另一图完全重合,那么这两个图是同构的。
- 必要条件 - 结点数相同、边数相同、度数相同的结点数相同
类型
- 零图:没有结点没有边
- 空图:边集合为空但结点集合可以非空
- 完全图:任何两个结点之间都有边相连
- 无向图/有向图/混合图:
- 无向图的邻接矩阵是对称矩阵
- 包含有向边和无向边的图是混合图
- 补图:由G的所有结点和构成完全图需添加的边所组成的图
- 简单图:两个结点之间可以只能存在一条边
- 多重图:两个结点之间可以有多条边
- 带权图/赋权图:边上有权重
- 标号图:边的权重用+-或01等二元表示
- 正则图:所有结点的度数都相同则为k-正则图
- 二分图:所有结点分为两个集合,每条边的两个端点分别在这两个集合中,同一集合的结点之间没有边相连
- 其他:
- 树与森林
- 树是特殊的无向图,没有回路
- 树的任意两点之间恰好有一条路径
- 森林由多个互不相连的树组成
- 生成树
- 包含图中所有结点的树型子树
- 带权图中,权重最小的生成树为最小生成树
- 斯坦纳树
- 带权图中,对于结点子集V,包含子集中所有结点且权重之和最小的子树即斯坦纳树
- ==与最小生成树的区别==:一个是针对结点子集,一个是包含所有结点
- 树与森林
连通性
- 相邻结点:一条边联结的两个点
- 相邻边
- 无向图:同一端点的两条边
- 有向图:一条边的终止结点必须是另一条边的开始结点
- 路径
- 依次遍历相邻边产生的结点序列
- 简单路径:不包含重复结点的路径(主要研究对象
- 回路:闭合的路径即为回路
- 通路
- 依次遍历相邻边产生的边序列
- 开通路/闭通路
- 通路长度:通路中遍历的边的数量
- 简单通路:每条边只遍历一次的通路
- 环路:闭合简单通路
- 哈密顿回路:遍历了图中所有结点的回路
- 从图中的任意一点出发,经过图中每一个结点当且仅当一次
- 欧拉回路:图中所有边只遍历一次
- 连通图/弱连通图/强连通图
- 强连通图:在有向图中,沿着边的方向前进时,任何两个结点存在有向路径
- 连通分支/强连通分支
- 针对子图而言
- 社会研究的一般性结论:一个图中只存在一个超大连通分支
- 最短路径
- 连通图中任何两个结点之间长度最短的路径为最短路径,其长度为该两个结点间的最短距离
- 平均路径长度:所有结点对的最短路径平均值
- n阶邻居:指所有到V的最短路径不大于n的结点
- 直径
- 图中任何两个结点之间最短路径的最大值为图的直径
- 注意:只定义在连通图中
- 桥
- 移除该边会导致图中连通分支增加
算法
随机游走算法
- 设置:
- 针对带权图
- 边的权重为遍历该边的概率
- 对于以$V_i$为起始的所有边,有:$\sum_x w_{i,x}=1$
- 算法:

深度优先/广度优先遍历算法
- 应用:爬取网站资源,爬取用户群体资料等
- 注意:由于社交网络挖掘中直接邻居比间接邻居更重要,所以一般用==广度优先==比较多
Dijkstra——最短路径算法
- 主要思想:不断更新到某个节点的最短路径
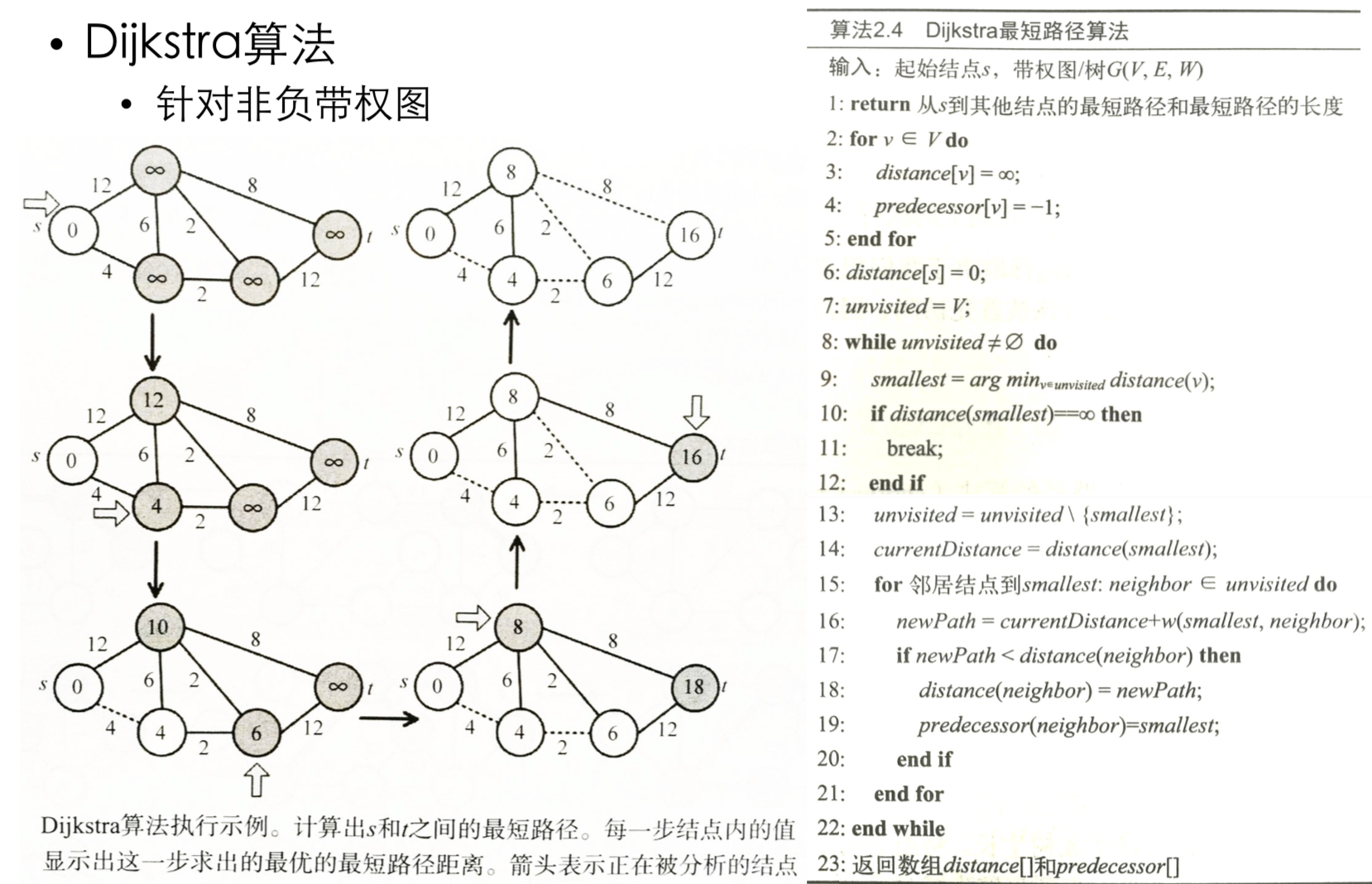
Prim——最小生成树算法
- 主要思想:分清楚已扩展结点和未扩展结点的相邻性
- 应用:成本最低的网络布线策略,社交网络信息传播路径等
- 算法:

Ford-Fulkerson——网络流算法
- 应用:下水管道网/手机短信传播网
- 流网络的形式化定义
- 前提:带权有向图G(V,E,C)
- 容量:限定了该边可以通过的流的最大值,反向流不存在
- 源点s与汇点t:s连接了无限供应的流
- 流守恒限制:对于除了s和t之外的图中所有结点,进入结点的流等于离开它的流
- 网络流量:源点的输出流减去流入源点的输入流,或流入汇点的输入流减去流出汇点的输出流
- 网络最大流算法的目的:发现使得每条边都拥有最大流量的分配方案
- 主要思想:利用残留网络和增广路径
二分图的最大匹配
- 应用Ford-Fulkerson最大流算法来寻找最大匹配
- 增加s和t结点,让s连接所有$V_{left}$结点,让t连接所有$V_{right}$结点
- 图中所有边的容量都为1
网络度量
中心性度量
度中心性
-
无向图:$C_d(v_i)=d_i$
-
有向图:
- 缺点:不能用来比较不同网络中的中心性值
度中心性的归一化
- 简单归一化:使用最大可能度数来进行归一化
- 采用最大度数进行归一化
- 采用度数和进行归一化
特征向量中心性
- 核心思想:通过邻居结点的重要性来概括某个节点的度中心性
- 注:A为邻接矩阵,$C_e$为$A^T$的特征向量,$\lambda$是$A^T$对应的特征值
- 计算:求邻接矩阵最大特征值对应的特征向量
- 计算方法:求解矩阵$A$的特征值$\lambda$(即解:$\det(A-\lambda I)=0$),取其中最大的特征值,代入之前的式子计算其对应的特征向量$C_e$,最终向量$C_e$就对应了图中的特征向量中心性。
Katz中心性
- 核心思想:加入偏差项来避免没有入度邻居的结点中心性为0的情况
- 注:$\alpha$为一个控制参数,实际上一般选择$\alpha<\frac{1}{\lambda}$,$\lambda$是$A^T$对应的特征值
- 计算:对特征向量中心性的优化,全部加一个偏差项$\beta$和常数项$\alpha$
PageRank中心性
- 核心思想:入度邻居贡献过来的中心性应当除以该邻居的出度
- 注:$D$是一个关于出度的对角矩阵,实际上一般选择$\alpha<\frac{1}{\lambda}$,$\lambda$是$A^TD^{-1}$对应的特征值
- 计算:为Katz中心性的优化
HITS算法(书上没有!)
- 核心思想:
- 权威值$a(i)$与中枢值$h(i)$
- 权威网页:与某个主题相关的高质量网页,入链数量(入度)很大
- 中枢网页:指向很多高质量(权威)网页的网页
中间中心性
- 核心思想:体现结点在链接其他结点时的重要性,即计算其他结点间的最短路径中通过该结点的路径数目
- 注:$\sigma_{st}$是结点$s$到$t$的最短路径数,而$\sigma_{st}(i)$是经过结点$i$的最短路径数
- 注2:无向图中,由于s到t和t到s可以被视为不同的路径,所以计算的时候要*2
-
注:归一化,用中间中心性除以它的最大值(当结点出现在连接任意结点对的所有最短路径中时)
-
直观上来感觉:连接的桥结点的中间中心性就比较大
接近中心性
- 核心思想:越接近图中心位置的结点越容易快速到达其他结点,即最中心结点应当具有到达其他结点的最小平均最短路径
- 注:$l_{v_i}$是结点与其他结点之间的平均最短路径
群体中心性
群体度中心性
- 核心思想:是群体外部的结点连接到群体内部结点的数目
- 也可进行最大值归一化
群体中间中心性
群体接近中心性
- 群体到元素的最短路径:最小/最大/平均
传递性与相互性
传递性
- 核心思想:我朋友的朋友也是我的朋友
图的聚类系数
- 注:三元组是三个结点的有序排列(ABC:边是A-B,B-C),通过两条边或三条边连接,一个三角形能找到三个不同的三元组
局部聚类系数
相互性
- 核心思想:如果你是我的朋友,那么我也是你的朋友
- 注:$Tr$是矩阵的对角线之和
- 计算:看邻居相连的比例
结构平衡与社会地位
结构(社会)平衡理论
-
核心思想
-
我朋友的朋友还是我的朋友
我敌人的敌人就是我的朋友
我朋友的敌人也是我的敌人
我敌人的朋友也是我的敌人
-
-
判断:在带有标识(符号)的有向图中,一个三元闭包(三角形)是结构平衡的,当且仅当$w_1w_2w_3 \ge 0$
-
推广:对于任意回路,如果边值乘积的结果是正的,那么这个回路就是社会平衡的
社会地位理论
-
核心思想:如果X的地位比Y高,Y的地位比Z高,那么X的地位应该比Z高
- 注意:同一个图,结构平衡理论和社会地位理论应用的结果相反
- 推广:对于n个结点的回路,如果有n-1条连续的边是正的,最后一条边是负的,则社会地位理论认为该回路是平衡的。
结点相似度度量
结构等价性度量
- 核心思想:关注共有邻居结点的数量
- 计算:==超多种公式!(看书和ppt==
规则等价性度量
- 核心思想:关注邻居结点的相似程度
- 模型:SimRank度量模型
- 关键:鉴于递归度量的计算代价比较高,可以做适当放宽
基于结点之间路径(书上没有!)
基于图嵌入的向量表示(书上没有!)

网络模型
网络属性
- 定义:能在不同网络中使用一致方法来计算的属性
度分布
-
定义:网络中结点的度数分布
- P(d)代表随机选择的结点v的度数为d的概率
-
大多数网络(包括社交网络)的度分布满足幂律分布
- 无标度网络
- 定义:符合幂律分布的网络
- 无标度网络中节点的度大致遵循“重尾”的幂律分布,这种分布没有特征尺度,所以称为“无标度”
- 启发:是否用中位数代替平均数来衡量会更好?
聚类系数
- 衡量网络的传递性
- 真实世界的社交网络中,具有较高的平均局部聚类系数
平均路径长度
- 衡量结点间信息传播路径的长短(可达性)
- 相关理论:小世界现象/六度分隔理论
总结
- 幂律分布、高聚类系数以及较短的平均路径长度,在真实世界网络中被频繁发现。
随机图模型
- 核心思想:网络图中任意两点间边的产生是随机的
两种模型
- $G(n,p)$模型和$G(n,m)$模型:

- 随机图定理:

- 随机图的演变:

- ==相变==:随机图的直径从最大值开始收缩时的拐点称作为相变点
- 定理4.4:随机图中,当$c=1$(结点平均度数)时,相变开始出现
随机图的属性
-
度分布
-
定理4.5:随机图G(n,p)中,结点v的度数$d_v=d$的概率是
-
结论
- 极限情况下,随机图的度满足泊松分布,这不同于在真实世界网络中观察到的幂律分布
-
- 聚类系数
- 定理4.6:随机图中结点v的局部聚类系数期望值为p
- 定理4.7:随机图中结点v的全局聚类系数期望值为p
- 平均路径长度
- 定理4.8:随机图的平均路径长度为$l=\frac{\ln \mid V \mid}{\ln c}$
总结
- 随机图准确地模拟了平均路径长度而低估了聚类系数
小世界模型
- 目的:应具有较短的平均(最短)路径长度和较高的聚类系数
规则格
- 每个节点都与K个最近邻节点相连(K为偶数
- 特点:具有较长的平均路径长度和较大的聚类系数
小世界模型构建
- 核心思想:对规则网采用边重连的方法,让规则网逐渐过渡到随机网络
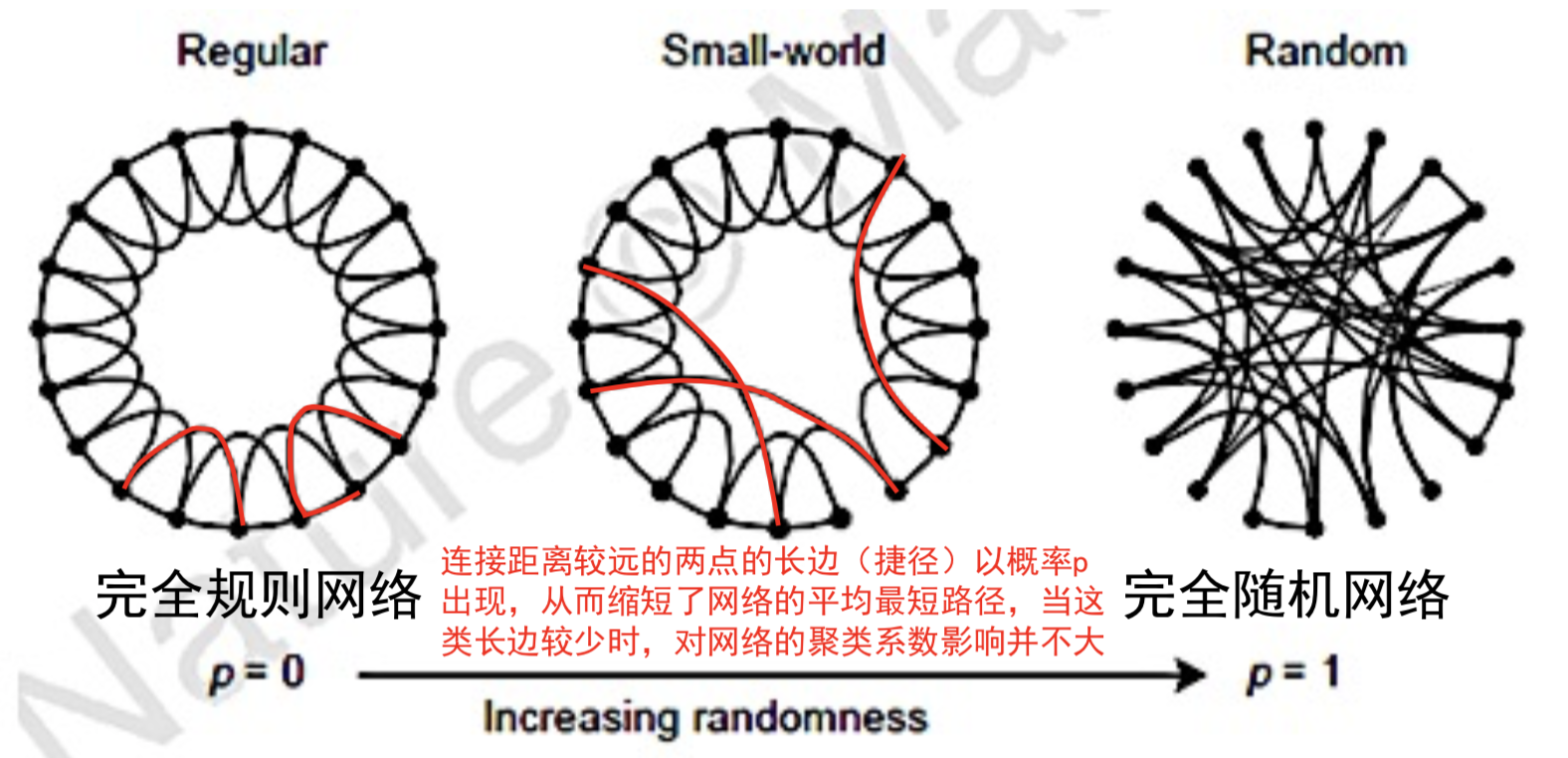

总结
- 根据小世界网络产生规则,大部分结点的度数相同,在度分布上并不符合真实网络中度的幂律分布
- 很多现实网络具有“小世界特征”
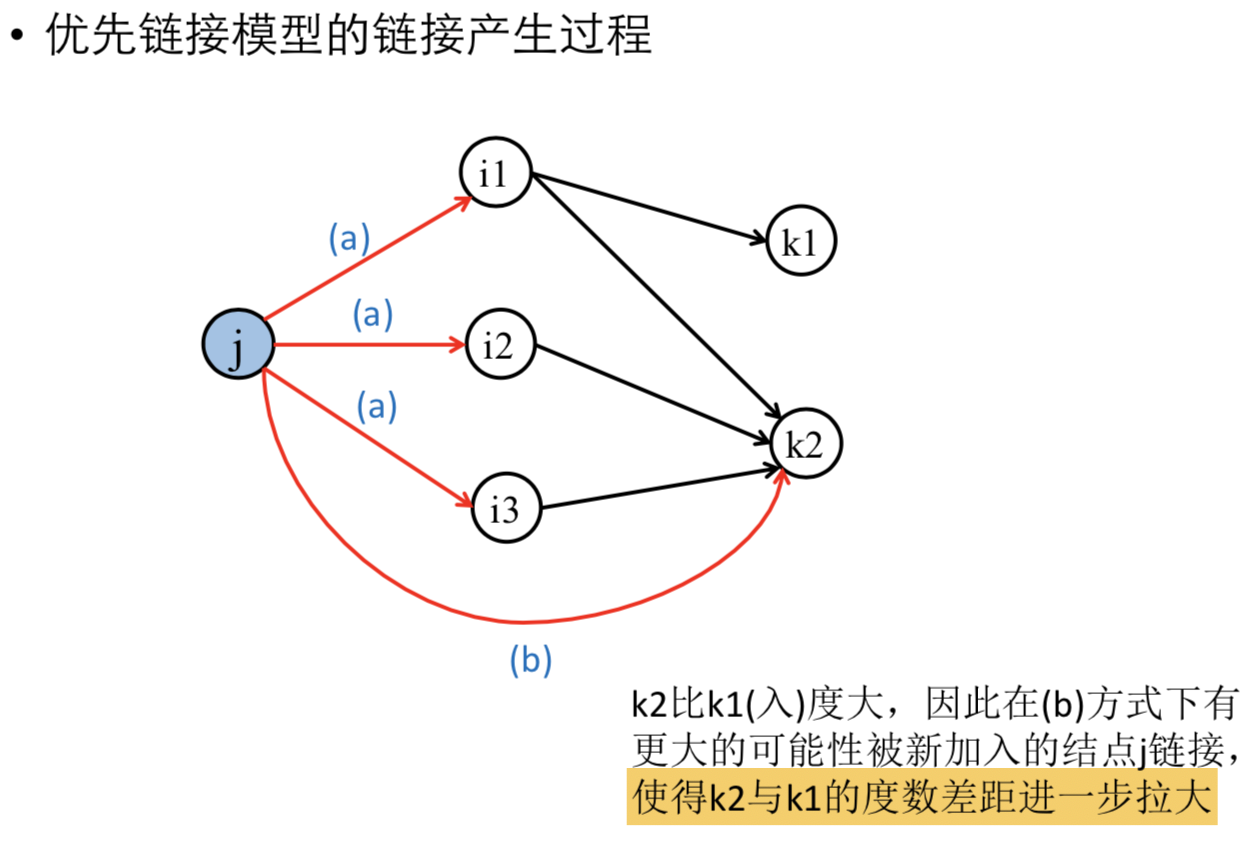
优先链接模型
- 核心思想:新加入网络的结点应该更倾向于连接到网络中有较多连接(度数较高)的结点
- 富者更富的马太效应
- 目的:解决度分布上不能很好模拟现实网络的缺点
- 缺点:网络虽然能较好地模拟平均路径长度短和度分布(优先链接模型网络的度分布满足幂律分布),但是聚类系数太小
网络流行度的马太效应(书上没有!)
- 入链分布为幂律分布佐证了马太效应(富者更富)和长尾现象的存在
- 优先链接模型产生的原理:网络中个体行为的选择并非完全自愿随机的,而是受其他个体影响,更容易倾向于复制他人的选择(随大流
数据挖掘概论
数据与特征
什么是数据挖掘
- KDD:从数据中提取有用的模式
数据来源
- 个人信息
- 好友信息
- 与物品(item)的“交互”数据
- 网络发言
数据获取方式
- 利用网站提供的API
- 利用爬虫程序
- 以用户为源头:选择种子用户然后利用BFS爬取邻居数据
- 以物品为源头:选择种子,收集与种子发生交互的用户,根据需要爬取这些用户的邻居数据或这些用户交互过的其他物品数据
- 利用可公开下载的数据源
- 与站方合作获取(包括购买)
数据的表示方式
- 格式化:e.g. 符合关系数据库的二维表
- RDF(资源描述框架)三元组:知识图谱常用的存储格式
数据特征类型
- 名词性/类别特征:字符串表示,相互间无法比较,无法加减乘除
- 序数特征:数值表示,可做排序,可比大小,但差值无意义
- 间隔特征:数值表示,差值有意义,但比例无意义
- 比例特征:数值表示,差值比例都有意义(即:可加减乘除)
文档向量模型
- 目标:将文本文档转换成(特征)向量
- $w_{ij}$反映关键词j对于文档i的刻画程度
- TF-IDF打分机制
- 目的:衡量一个词语对于一篇文档的相关程度$w_{ij}$
- 原理:一个词对于一篇文档的重要程度与其在该篇文档中出现的次数成正比,但与它在整个语料库(文档集合)中的出现频率成反比
- 公式:$w_{ij}=tf_{ij}\times idf_{j}$
- $tf_{ij}$是词j在文档i中出现的频率
- $idf_{j}$是词j在全文集上的逆文本频率
数据质量检测
- 噪声:【准确性】
- 异常值:【一致性】
- 缺失值:【完整性】
- 缺失值太多就反映出数据稀疏性问题
- 重复数据
数据预处理
- 数据聚合:多个特征合并成单个特征
- 数据集成:将来自多个数据源的数据统一表示
- 数据离散化:将连续值转化成离散值
- 特征筛选:找出关键特征(PCA)或选取与模型目标相关特征
- 特征提取:将原来的特征集转化成新的特征集
- 数据采样
- 随机采样
- (不)重复采样
- 分层采样:适用于类别属性分布不均的样本
- 大规模社交网络的用户采样
频繁模式挖掘(书上没有!)
- 也称为关联规则挖掘,频繁模式则是频繁地出现在数据集中的模式
关联规则的形式化表示

频繁模式挖掘的步骤
- 找出所有频繁项集:项集出现次数不少于最小支持数min_sup
- 当一个项集是频繁的,则它的任何非空子集都是频繁的
- 频繁项集产生强关联规则:规则必须满足最小支持度和最小置信度
Apriori算法

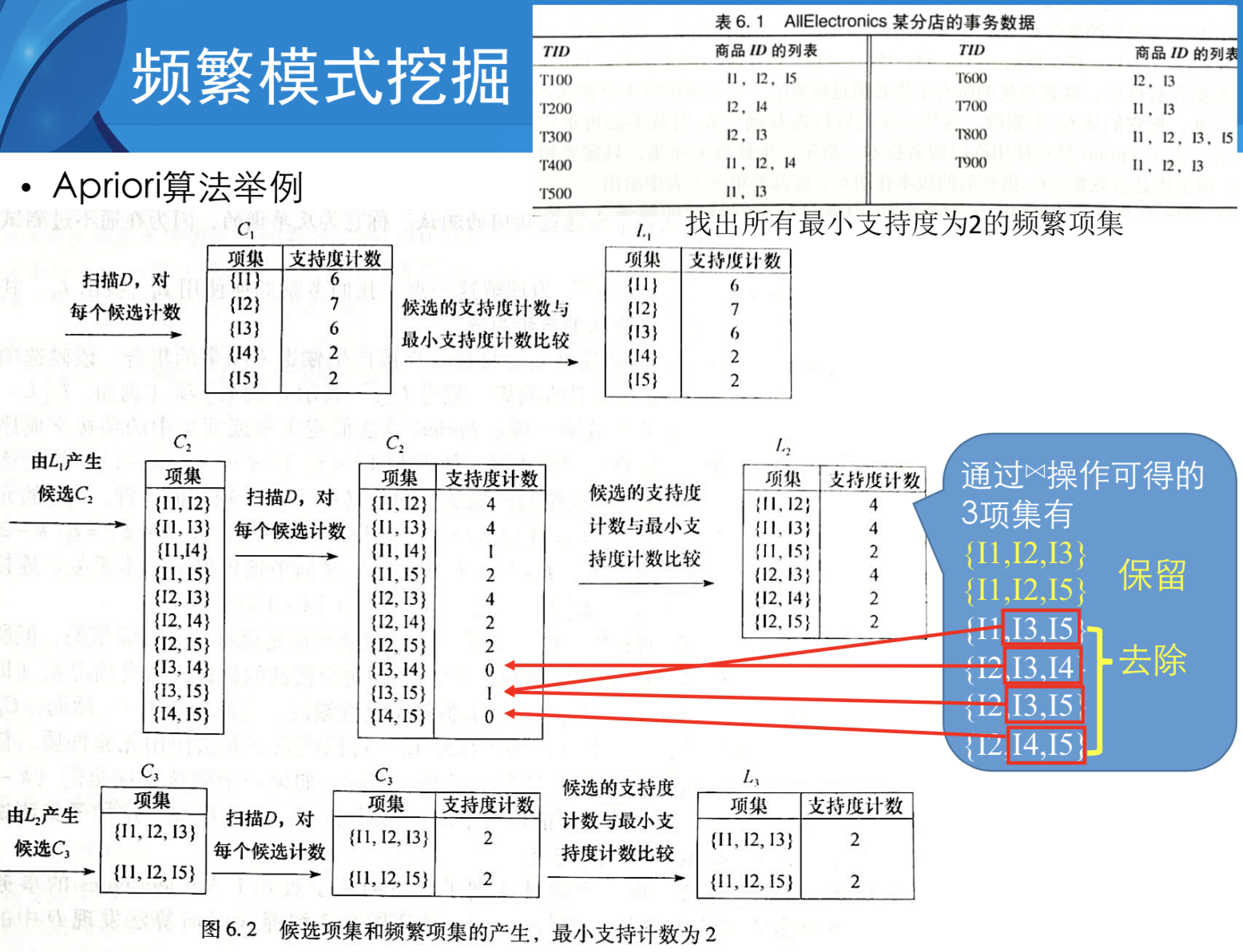
监督学习
- 算法总结:
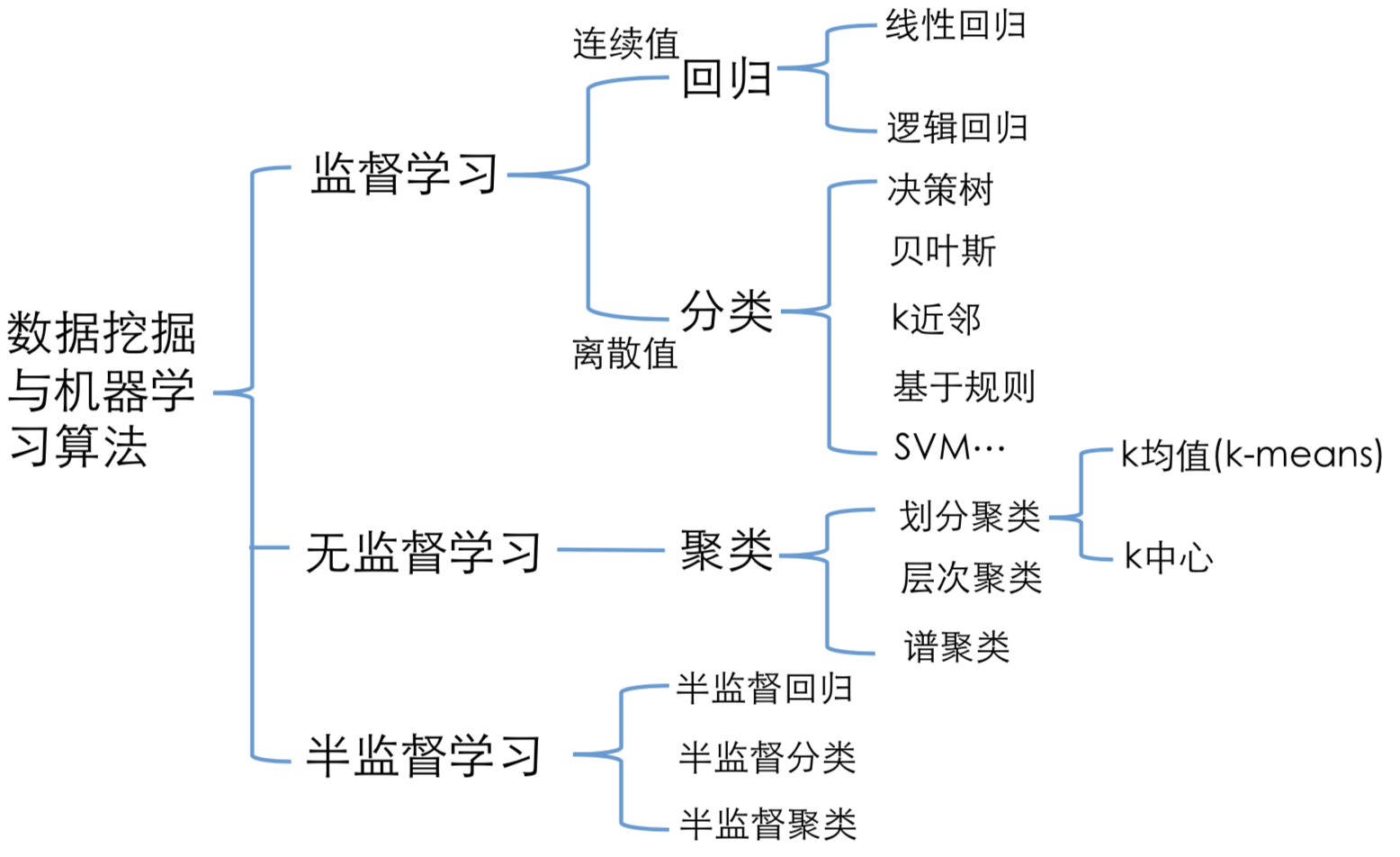
分类算法 (离散值)
- 决策树分类
- 方法:自顶向下递归构建树
- 终止条件:叶子结点以外的每个结点都代表一个分类特征,当某个分支下的样本集合是纯净子集时则不再分割该子集而是创建叶子结点
- 纯净子集的衡量:信息熵$entropy(T)=-p_+\log p_+-p_-\log p_-$
- 在纯净子集中,所有实例的类别属性都是相同的,信息熵为0
- K-最近邻分类
- 核心思想:一个样本在特征空间中的k个最相似样本中的大多数所属的类别代表该样本的类别
- 重点:k值的选取
- 基于社交辅助的分类
- 核心思想:【社会影响与同质性】
- 注:该思想与推荐算法中基于用户的协同过滤思想一致
- 算法描述:

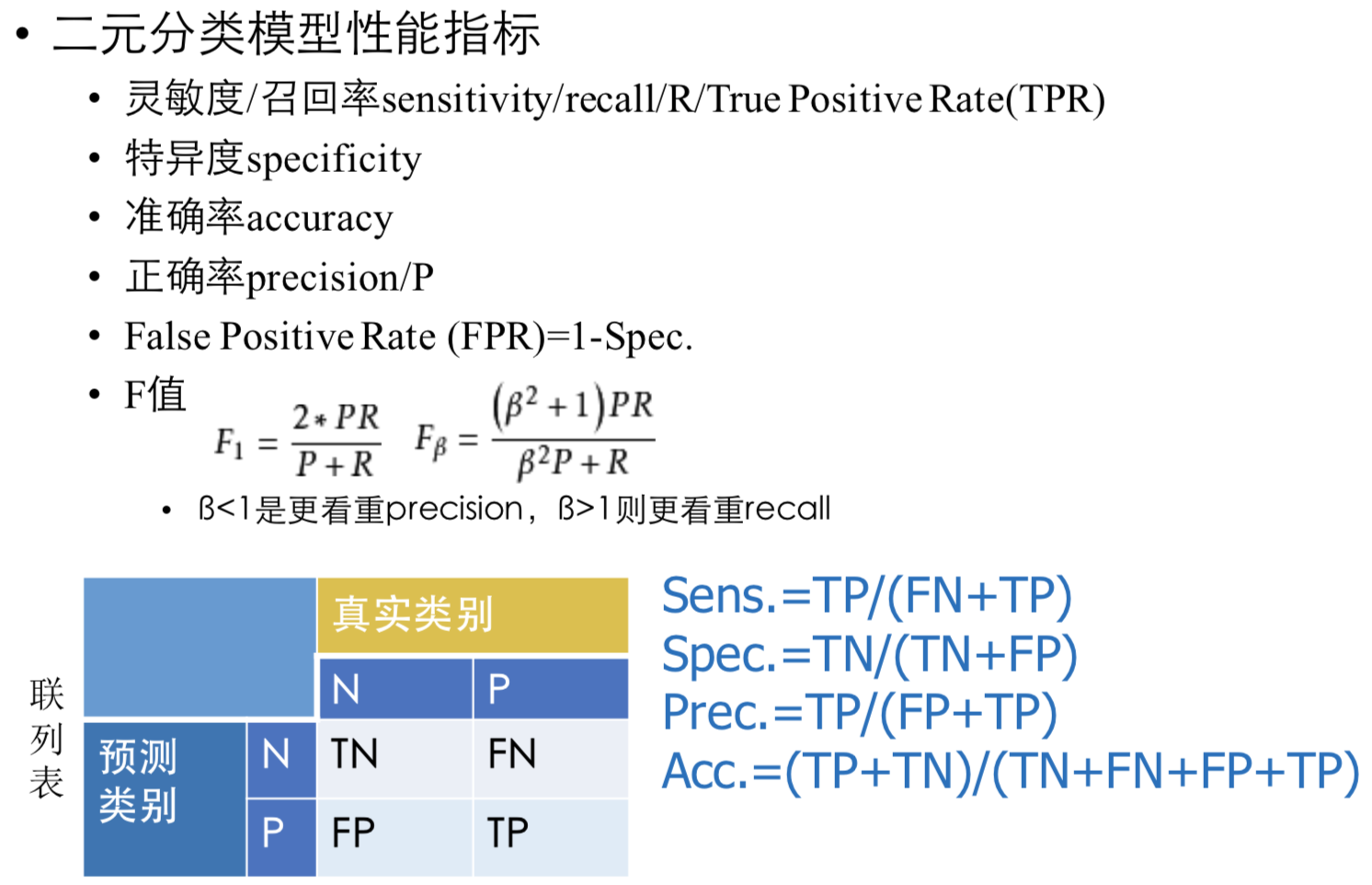
- 分类性能指标:
回归算法 (连续值)
- 线性回归
- 参数估计:最小二乘法或最大似然估计
- 逻辑回归
- 参数估计:最大似然估计
- 回归性能指标:平均绝对差 均方误差 均方根误差
训练集和测试集的生成
- Leave-one-out
- K-fold cross validation
非监督学习聚类算法
- 距离度量:马氏距离、曼哈顿距离、欧式距离、余弦距离
- K-means算法
- 初始的k个中心点的选取不同则聚类的结果不同
- 层次聚类:凝聚法(书上没有!)
- 聚类效果评估(各种距离平方和)
- 内聚性:簇中实例相互间距离越近越好
- 离散性:簇与簇之间的距离越远越好
- Sihouette指数:结合了内聚性和离散性
- ==例题!==
社区挖掘
社区的定义
构成社区的要素
- 至少由2个结点构成的集合
- 结点具有相似性(如:兴趣相同)
- 结点间基于共同兴趣等因素产生交互
社区的分类
- 显式社区
- 隐式社区
- 社区成员以一种未承认的社区形式进行交互
- 豆瓣上喜欢/评论同类电影的用户可视作构成一个社区
社区发现
基于成员的社区发现
- 基本思想:将具有相似特征的成员归于统一社区
- 可以考虑的成员特征类型
- 结点相似度
- 结点度
- 结点可达性
基于结点度相似的社区发现
- 基本思想:搜索网络中的团
- 团是完全子图(而完全图需要包括全部结点集
- 团中的结点度数为k-1(k是团的结点数)
- 算法思想
- 暴力搜索:对于大规模网络的搜索代价太大
- 思想:放入一个结点,则将它的邻居也全部一起放进去
- 剪枝搜索:删除度数小于k-1的结点
- 问题:团的要求太高
- 简化团搜索:k簇
- K越大,k簇的要求就越低,搜索空间就更小
- 对度数的要求放宽成$n-k$
- 将团作为一个更大社区的种子:团过滤算法(CPM)
- 思想:给定n,先找出所有大小为n的团,然后把每一个团作为结点,若两团共享$n-1$结点则连边,生成一个团图
- 暴力搜索:对于大规模网络的搜索代价太大
基于结点可达性的社区发现
- 基本思想:两种极端可达性
- 任意两个结点都有路径相通
- 任意两个结点都是邻居
- 新的社区子图定义:k-团、k-club、k-clan
- 最大连通子图且最短路径小于等于k(路径结点不一定在团中)、连通子图且最短路径小于等于k(路径结点都应该包含在子图中)、同时满足团和club的约束条件
概念总结
| 概念 | 定义 | 关系 |
|---|---|---|
| 团 | 完全子图,包括结点子集$V$中的所有结点,每个结点的度数都为$\mid V\mid-1$ | |
| K簇 | $d_v\ge \mid V\mid-k, \forall v \in V$,V是簇的结点集合 | 1簇是一个团 |
| K-团 | 最大连通子图,任意两个结点间的最短路径小于等于k | 两个结点间的最短路径上的结点不一定包含在团中 |
| K-Club | 连通子图,并且最短路径上的结点都应该包含在子图中 | |
| K-Clan | 同时满足k-团和k-club的约束条件,子图所有的最短路径长度小于等于k | K-clan = k-团 $\cap$ k-club |
基于结点相似度的社区发现
- 基本思想:相似的结点属于同一个社区
- 结构对等性与规则对等性
基于群组的社区发现——社区本身有特殊形式
均衡社区发现——最小割
- 核心思想:找割,希望割后的社区相对均衡且割尽可能小
- 比例割目标函数——考虑结点数
- 归一化割目标函数——考虑度数的总和
- 算法:谱聚类求近似解
层次化社区发现——移除桥
- 边介数:最短路径经过该条边的节点对数量
- 算法:自顶向下的聚类算法==(难算!)==,移除最大边介数,迭代。
稳定社区/模块化社区/高密度社区发现(略)
社区演变
- 三类常见的社区演变模式:分裂、致密化、缩径
- 网络分裂
- 大规模网络随时间推移分解成三个部分:巨大结构、星状结构、单元素
- 图的致密化
- 图的密度随网络增长而变大,即边数的增加快于结点数的增加,$\mid E(t) \mid \propto \mid V(t) \mid^{\alpha}$
- $1\le\alpha\le2$,$\alpha=2$时产生团(因为团是一个最大完全子图
- 图的缩径
- 随着网络边的增加,网络图的直径在不断收缩
社区评价
四种量值
- TP: 相似的成员被划分到同社区/正确地分到同个
- TN: 不相似的成员被划分到不同社区/正确地分到不同个
- FP: 不相似的成员被划分到同社区/错误地分到同个
- FN: 相似的成员被划分到不同社区/错误地分到不同个
- 准确率$P=TP/(TP+FP)$
- 召回率$R=TP/(TP+FN)$
- $F1=2*PR/(P+R)$
- ==例子!==
纯度
- 标签与社区大部分结点标签相同的结点比例 $=\frac{1}{N} \sum_{i=1}^k \max_j \mid C_i\cap L_j \mid$
归一化互信息
- 公式:

- NMI接近1则表明发现的社区和真实的社区具有较高的相似度
无监督时基于聚类质量方法的评价
- 基于语义
- 基于聚类质量方法
社交网络的信息传播
- 定义:通过社交网络中的个体间的交互行为,将一条信息(知识、创新、产品等)传播并到达多数个体的过程
- 三要素:传播者、接受者、传播媒介
计算传播学基本原理(书上没有!)
信息传播模型
羊群效应(Herd Behavior)——显示网络、全局信息
- 定义:个体观察所有其他行为后,采取与其一致的行为效应
- 两个关键因素
- 个体之间的相互联系
- 个体之间转移行为或观察行为的方法
- 四个实验条件
- 一个待做的决定
- 个体的选择决定需要遵从一定的顺序
- 个体是在掌握一定的信息后才做出决定
- 个体之间无法传递信息
- 个体无法知道他人掌握的信息,但是可以通过观察他人行为来推断他人掌握的信息
- 贝叶斯建模:通过计算条件概率,选择概率最大的情况就会导致羊群效应的产生
- 干预手段:向要做出选择的个体提供更多的信息
信息级联(Information Cascade)——显示网络、局部信息
- 定义:信息或决策在一群个体中扩散的过程
- 两个条件
- 个体通过网络相连接
- 个体只能观察到其近邻(好友)的决策行为
独立级联模型(ICM)
- 四个假设
- 网络图中的结点表示行为的执行者,边表示邻居关系
- 每个结点只有活跃或不活跃两种状态,被激活的结点表示该结点采纳了某种行为/创新;活跃结点可视为信息发布者,被激活结点可视为接收者
- 一个结点在t时刻被激活后便可以在t+1时刻激活它的一个邻居结点,激活概率为$p_{v,w}$
- 激活是一个渐进过程,结点只能从不活跃跳转到活跃状态,反之不行
- ICM模型表示信息传播是以发布者为中心的,结点的激活过程是随机过程
级联范围最大化
- 目标:初始时用最少的激活结点达到最终时激活最多的结点
- 算法
- 形式化定义:S表示初始激活结点集合,f(S)表示最终能激活的结点集合,则算法目标是,对于给定的预算k,找到合适的S,使得$\mid S\mid =k$,$\mid f(S) \mid$最大
- 由于f(S)是次模函数,该问题是NP难问题
- 使用贪心算法构建S以得到近似的最优解
- ==例题==
- 干预
- 限制信息(决策)发布者的出链
- 限制接收者的入链
- 降低网络结点(个体用户)的激活概率$p_{v,w}$
线性阈值模型(书上没有!)

创新扩散(Innovation Diffusion)——隐式网络
-
特征:高度可见、有相对优势、与其所处的社会文化规范相容、复杂度不能过高
- 采用者模型
- 五种类型的采纳者:创新者/早期采用者/早期采用人群/后期采用人群/迟缓者
- 两级传播模型
- 大多数信息源自大众媒体,并且直接面向意见领袖
- 随后意见领袖再扩散这些信息
- 创新扩散过程
- 了解阶段:接触新鲜事物,但知之甚少
- 兴趣阶段:发生兴趣,并寻求更多的信息
- 评估阶段:联系自身需求,考虑是否采纳
- 试验阶段:观察是否适合自己的情况
- 采纳阶段:决定在大范围内实施
- 创新扩散过程建模
- 外部影响力模型

- 内部影响力模型

- 混合影响力模型

- 外部影响力模型
- 干预
- 限制(新)产品或用户的分布
- 降低用户对产品的兴趣
- 减少用户之间的沟通
流行病/传染病模型(Epidemic Model)——隐式网络
- 三个要素:病原体、宿主、传播/感染机制
- 假设:人与人之间关系未知(存在隐性网络),注重研究全局模型而非观察具体传播路径
- 模型:
- SI、SIR、SIS、SIRS
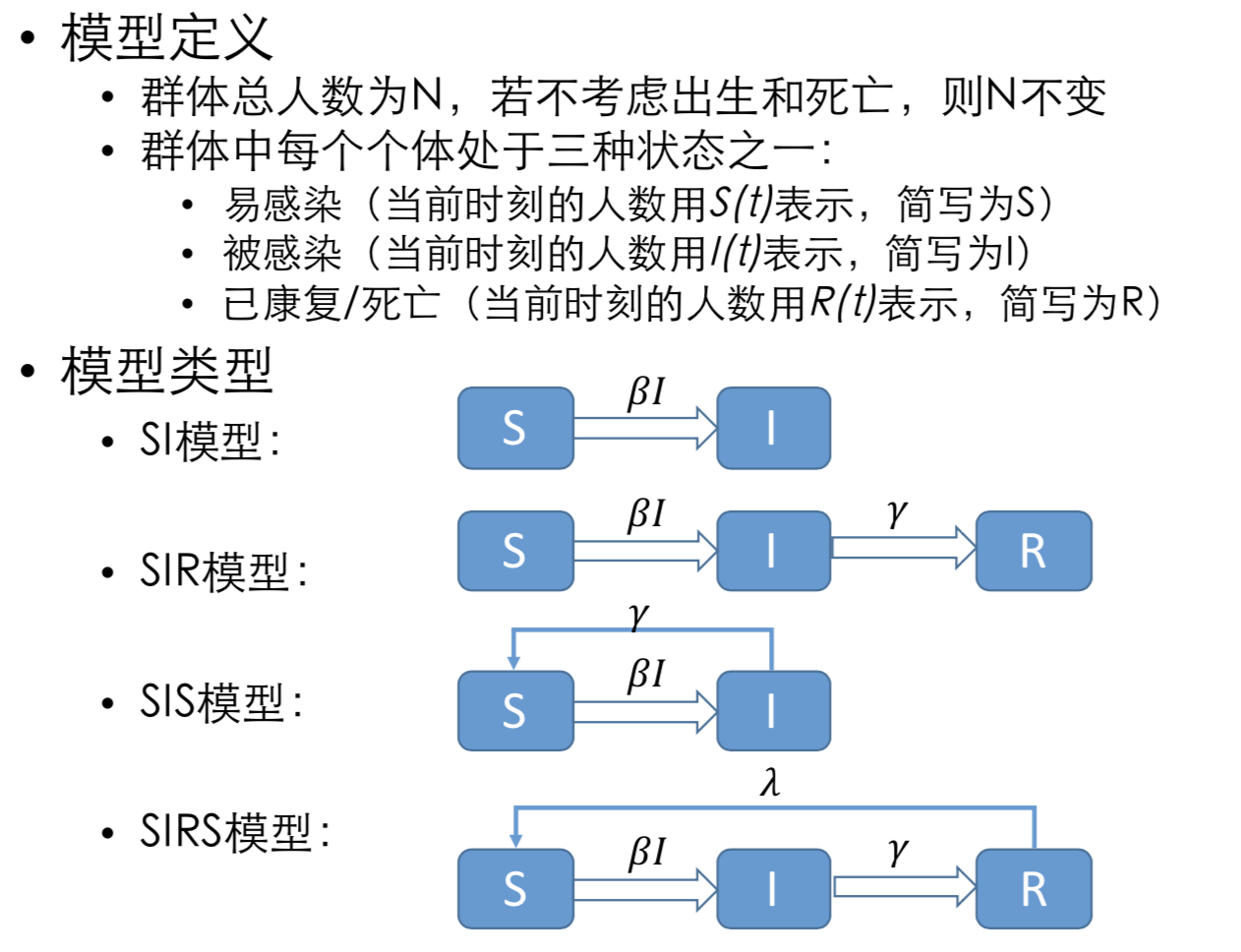
- ==微分方程需要掌握吗?==
- 干预
- 对社交频繁的人接种疫苗
- 群体免疫:对整群体内96%的随机个体接种疫苗达到群体免疫或者先对群体内30%的随机个体接种疫苗,再找到他们擅于交际的朋友进行接种
- 对被感染者和易感染者进行免疫隔离
影响力最大化(书上没有!)
- 目标:找到一组数量为k的种子结点,使得信息传播结束后网络中活跃的结点数最多(类似于级联范围最大化
- 算法
- 启发式算法
- 基于High Degree:选择度数最多的那些结点
- 不一定最优,因为这些结点可能处于一个团体中(富人俱乐部
- 基于Distance Centrality:选择那些与其他结点平均距离最短的结点
- Random:随机选择k个
- 基于High Degree:选择度数最多的那些结点
- 贪心算法:

- 改进的贪心算法:

- 启发式算法
信息覆盖最大化(书上没有!)
- 活跃结点:接收消息并传播的结点;
- 非活跃结点:不会传播的结点
- 消息结点:能看到信息的结点
- 真·非活跃结点:啥也不知道
- 目标:寻找k个种子结点,产生最多的活跃结点和消息结点
影响力和同质性
引言
- 同配网络
- 相似个体比不相似个体更容易形成连接
- 形成同配网络的三种动力
- 影响力、同质性、混杂
- 影响力和同质性的图示:
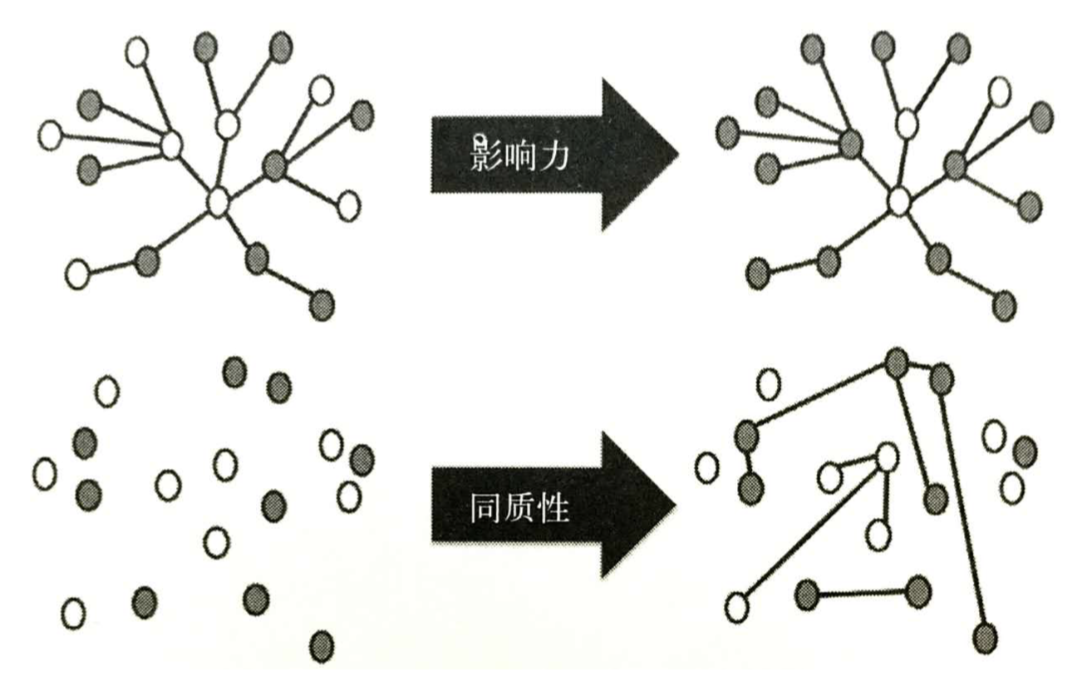
- 影响力和同质性的区分
- 影响力促使“好友变得相似”,而同质性使“相似个体变成好友”
度量同配性
度量符号属性的同配性
- 模块度
- 同配性意义值=同配性值(同种类结点间的边的比例)-期望值
度量序数属性的同配性
- 皮尔逊相关系数
==全是公式!应该会考!但是也太难算了吧 QAQ==
影响力
- 定义:在没有明显的强制措施和直接命令的情况下影响他人的行为或能力
度量影响力
基于预测的方法
- 通过度量网络中结点的中心性值(参考第三章)来预测该结点的影响
基于观察的方法
- 不同的场景中有不同的度量方法
- 将个体作为榜样:受榜样的个人魅力、学识等属性影响的观众人数来量化影响力
- 个体是被传播的对象:传播的级数、受众数量/比例等来量化影响力
- 个体的参与提升了某事物或行为的价值:购买了某商品的用户会提升该商品的价值(使其更容易被其他人接受),所以用价值的提升量/提升率来量化影响
社会影响力度量应用案例
- 博客圈:

- Twitter用户:

影响力建模
显式网络的影响力建模
隐式网络的影响力建模
- 参数估计
- 假设一个非参数函数去顾及影响力函数的形式(线性影响力模型)
同质性
- 定义:相似的人有成为朋友的趋势。
- 意义:同质性是同配网络形成的主要原因。
- 计算:

- 建模:把足够相似的结点连接起来

区分影响力与同质性
- 三个测试:洗牌测试、边缘反转测试、随机化测试
- ==要掌握吗?感觉要背的东西很多!==
用户行为分析
个体行为分析
- 个体在线行为分类
- 用户-用户行为、用户-社区行为、用户-实体行为
- 四要素
- 可观察的行为
- 如加入社团、建立好友关系等
- 特征
- 如已加入社团的好友数
- 特征-行为关联
- 例如通过分类决策树来找出影响用户行为的最关键特征
- 评估策略
- 可观察的行为
用户加入社区的行为分析
- 特征选择
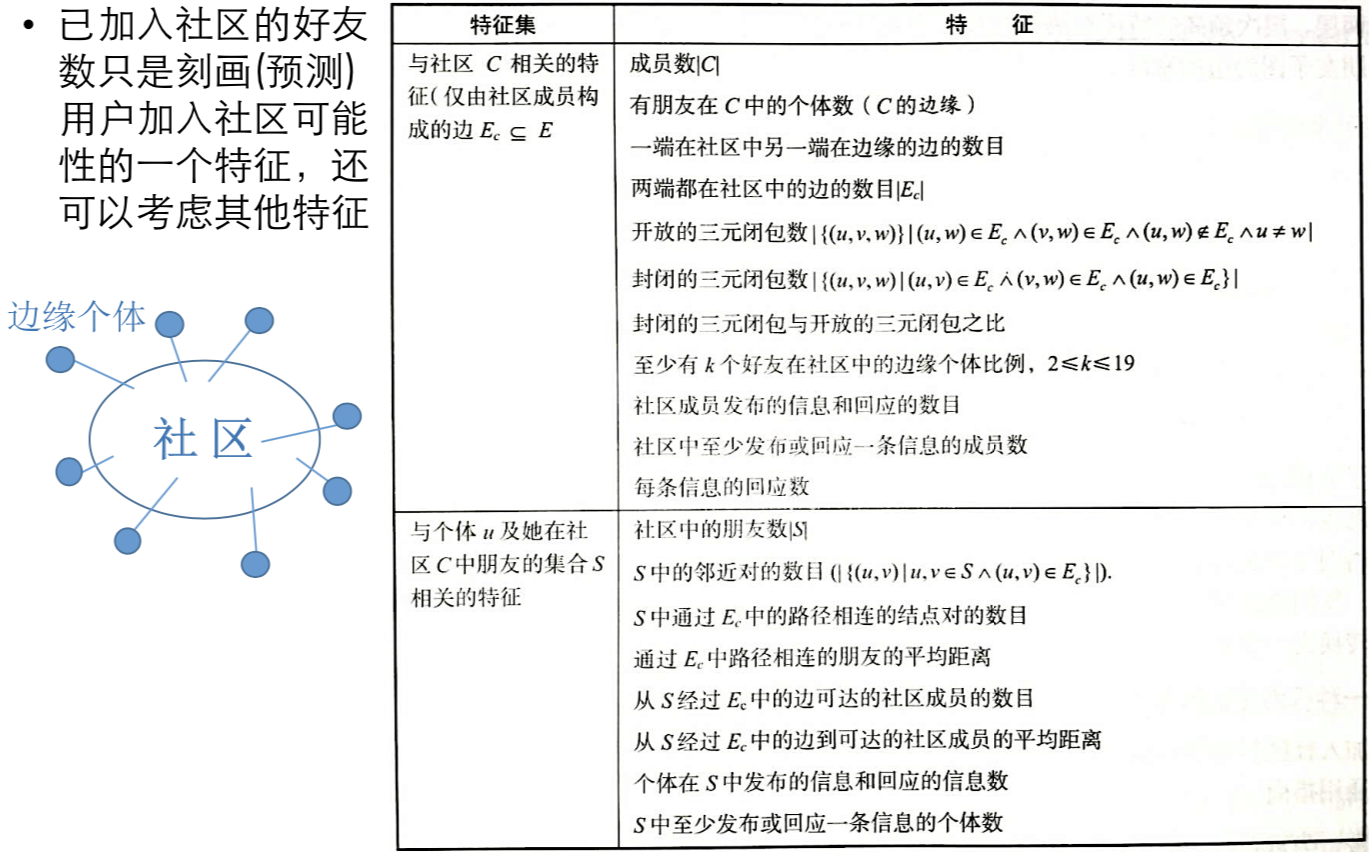
- 特征选择算法可以帮助你找到影响用户加入社区的关键特征
个体行为建模

个体行为预测

结构等价性度量
- 核心思想:基于个体之间共有邻居结点的情况来度量


规则等价性度量
- 核心思想:更关注邻居结点的相似程度
- 代表模型:SimRank
- 基于邻居结点之间的相似度来递归定义两个结点的相似度
- 鉴于递归度量的计算代价较高,可以做适当放宽
基于结点之间路径

群体行为分析
- 定义:指一个群体中的个体表现出相似的行为方式,这种相似行为可以是计划并协调好的,也可以是自发形成的
- 方法:将群体分成多个个体,对这些个体单独分析后,将分析结果汇聚成群体的行为结果
群体迁移行为

- 迁移行为的特征
- 网站用户活跃度
- 越活跃发生迁移行为的概率越低
- 用户社交圈的大小
- 在某一网站的社交圈(好友数)越多,发生迁移行为的概率越低
- 用户的等级
- 等级(地位)越高,发生迁移行为的概率越低
- 网站用户活跃度
群体行为建模
- 线性/逻辑回归模型
- 网络模型
- 小世界模型
- 侧重表达较小的平均最短路径
- 优先链接模型
- 侧重表达幂律分布
群体行为预测
-
概括:通过对预测的个体行为进行汇总来预测群体行为,该方式代价太大,通常是将群体(具体相同属性的个体集合)作为个体整体来预测
-
案例分析:三类人群的社交特性分析
用户画像简介
用户画像过程

博弈论基础
社交媒体中的推荐
推荐系统简介
- 本质:将用户和物品联系起来
- 定义
- 一个推荐算法可以理解为学习如下函数:$f:U\times I \rightarrow R$
- 函数值刻画了用户U对物品I感兴趣的程度
- 应用
- 电子商务、内容消费平台、扩展阅读、智能搜索、位置服务、精准广告…
- 挑战

经典推荐算法
协同过滤
基于记忆的协同过滤
- 定义:基于历史的评分记录
基于用户的协同过滤
- 定义
- 基于用户的历史评分记录来刻画用户间的相似性,相似用户对某项目的评分可以作为目标用户对该项目的评分依据
- 计算

基于项目的协同过滤
- 定义
- 基于项目历史的被评分记录来刻画项目间的相似性,目标用户对相似项目的评分可以作为目标用户对本项目的评分依据
- 计算
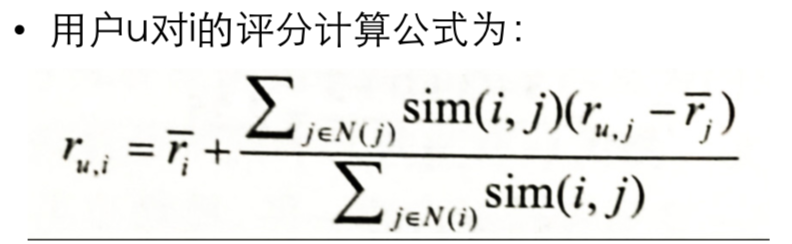
基于模型的协同过滤
- 定义
- 学习出能刻画用户评分行为的模型
基于SVD的推荐算法
基于矩阵分解(MF)的推荐算法
基于内容的推荐
群体推荐
- 基本思想:综合群组中每个用户的项目评分???
基于社交网络的推荐算法
单独使用社会信息
使用评分记录和社会信息
推荐性能评价
预测项目评分的性能评价

推荐项目是否相关的性能评价
- Precision
- Recall
- F值
- 看中相关项目排序位置的性能指标
- 基本思想
- 结果列表中排在前面的项目容易得到用户的关注,因此好的推荐算法应该将最相关的项目排在前面推荐出来
- Reciprocal Rank:第一个相关项目的rank倒数
- AP (Average Precision):

- nDCG (normalized discounted calculate gain):

- 基本思想
推荐项目的排序性能评价
评价指标考虑的其他方面
推荐的真实答案(用户喜欢的项目)获取
案例分析
-
Flickr社交网络分析
-
Twitter社交网络分析
-
微博好友推荐
-
豆瓣电影推荐
